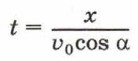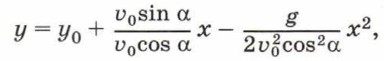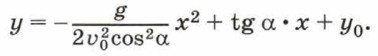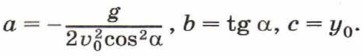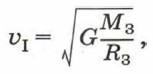Главная >> Физика. 10 класс. Базовый уровень. Пурышева

Глава 3. Следствия классической механики

Баллистика

Используя систему кинематических уравнений (1) и (2), можно рассчитать различные параметры полёта, например время полёта, максимальную высоту и дальность. Так, время полёта можно вычислить из уравнения (2), учитывая, что в момент падения у = О, и решив получившееся квадратное уравнение. Поскольку это уравнение имеет два корня, то, вычислив их, выбирают только тот, который не противоречит смыслу физической величины «время»: корень не может быть отрицательным. Подставив полученный результат в уравнение (1), можно вычислить конечную координату тела х, а значит, и дальность полёта.

Для того чтобы установить, по какой траектории движется тело, выразим время t из уравнения (1):

и подставим его в уравнение (2). Получим:

или

Полученная зависимость у = ƒ(x) имеет вид:

у = ах² + bх + с,

где а, b и с — постоянные коэффициенты, в нашем случае равные:

Из курса алгебры вам известно, что графиком такой зависимости является парабола. Следовательно, траекторией тела, движущегося под действием только силы тяжести, является парабола.

При реальных баллистических расчётах учитывают сопротивление воздуха движущемуся телу, поскольку при значительных скоростях это сопротивление оказывается весьма существенным. Даже для артиллерийского снаряда, имеющего специальную обтекаемую форму, реальная дальность полёта может получиться в 2—3 раза меньшей, чем рассчитанная без учёта сопротивления воздуха.

Решая баллистические задачи для межконтинентальных ракет, уже нельзя не учитывать шарообразность Земли. Траекторией движения такой ракеты, согласно первому закону Кеплера, является эллипс, один из фокусов которого находится в центре земного шара (рис. 52).

Космические скорости

3. Движение космических аппаратов происходит по тем же законам, что и движение естественных небесных тел.

Вам уже известно условие, при котором тело может стать спутником Земли: скорость такого тела должна быть не меньшей, чем круговая. Рассчитаем круговую скорость спутника Земли, считая расстояние между Землёй и спутником равным среднему радиусу Земли R_З:

где М₃ — масса Земли.

<<< К началу      Окончание >>>