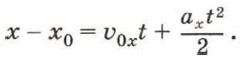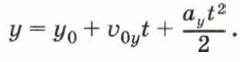|
|
|
|
|
Глава 1. Механические явления Путь и перемещениеРасчёт перемещения и координат3. Вспомним, что в зависимости от характера изменения скорости тела механическое движение может быть равномерным или неравномерным.
Если же тело за равные промежутки времени совершает разные перемещения, то движение является неравномерным. Наиболее простым случаем неравномерного движения является равноускоренное движение.
Как вам известно, формула для расчёта перемещения при равноускоренном движении имеет вид:
где Найдём проекцию вектора перемещения
Обратим внимание, что левые части выражений (1) и (3) равны. Следовательно, равны и их правые части:
Из полученного равенства выразим координату х и получим формулу для расчёта координаты тела через время t после начала движения. Такую зависимость называют уравнением движения.
Аналогично можно получить выражение для координаты у:
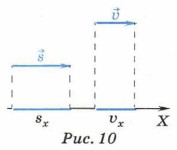
Наиболее просто использовать формулу (4) при прямолинейном движении, когда есть возможность направить ось X вдоль вектора перемещения (рис. 10).
В случае, когда тело движется равномерно прямолинейно, его ускорение а равно нулю. Подставляя это значение в формулу (3) и учитывая, что скорость не изменяется, т. е. υ = υ0, получаем формулу для расчёта проекции перемещения при равномерном прямолинейном движении: sx = υxt.
|
|
|



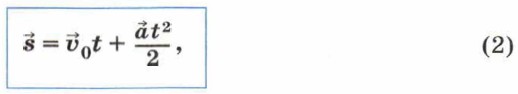
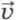 0 — начальная скорость тела,
0 — начальная скорость тела, 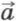 — ускорение тела.
— ускорение тела.
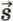 на ось ОХ (см. рис. 9, б). Из выражения (2) следует, что проекция sx равна:
на ось ОХ (см. рис. 9, б). Из выражения (2) следует, что проекция sx равна: