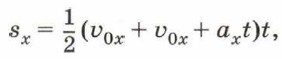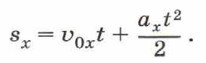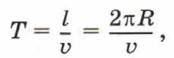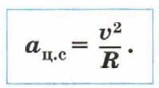|
|
|
|
|
Глава 1. Механические явления УскорениеДля доказательства этого предположения рассмотрим малый отрезок времени Δt внутри промежутка Ot. Чем меньше Δt, тем больше оснований утверждать, что за это время скорость тела не изменяется (вспомним определение мгновенной скорости). Поэтому за время Δt движение можно считать равномерным, и значение проекции перемещения равным площади соответствующего прямоугольника. Поскольку площадь рассматриваемой трапеции равна сумме площадей этих прямоугольников, то значение проекции перемещения также равно этой площади. Из курса геометрии известно, что площадь трапеции равна произведению полусуммы её оснований и высоты. В нашем случае основания равны υ0x и (υ0х + axt), а высота t. Следовательно,
или окончательно получаем формулу для расчёта проекции перемещения при равноускоренном движении:
Линейная скорость. Период. Центростремительное ускорение3. Напомним, что если тело разгоняется или тормозит, двигаясь по прямой, то векторы ускорения и скорости направлены вдоль этой прямой. Если же векторы скорости и ускорения направлены под углом друг к другу, то это означает, что скорость изменяет направление: тело поворачивает, т. е. движется криволинейно. Наиболее простым случаем криволинейного движения является движение по окружности с постоянной по модулю скоростью. Так движутся, например, скамейки на вращающейся с постоянной скоростью карусели или бегут дрессированные животные вдоль бортика цирковой арены. Мгновенную скорость, с которой тело движется по окружности, называют линейной скоростью. Если при движении по окружности модуль линейной скорости υ остаётся неизменным, то каждый оборот тело совершает за одно и то же время, называемое периодом обращения Т. Чтобы рассчитать период обращения, следует путь l, проходимый телом за один полный оборот, разделить на линейную скорость. Поскольку этот путь равен длине окружности, по которой движется тело, то период равен:
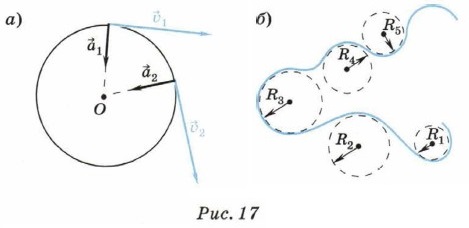
где l = 2πR — длина окружности, R — её радиус. При движении по окружности с постоянной по модулю скоростью направление линейной скорости непрерывно изменяется. При этом в каждой точке окружности ускорение направлено вдоль радиуса окружности к её центру (рис. 17, а).
Из курса физики основной школы вам уже известно, что такое ускорение называют центростремительным ац.с, и его модуль можно рассчитать, зная радиус окружности R и модуль линейной скорости υ.
Любое криволинейное движение можно с достаточной степенью точности представить как движение по окружностям разных радиусов (рис. 17, б). Поэтому формулу центростремительного ускорения можно применять в случае любого криволинейного движения с постоянной по модулю скоростью, подставляя в неё значение радиуса, соответствующее кривизне того или иного участка траектории.
|
|
|