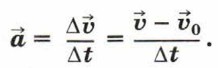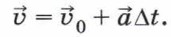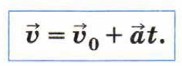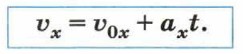Главная >> Физика. 10 класс. Базовый уровень. Пурышева

Глава 1. Механические явления

§ 8. Ускорение

Ускорение при равноускоренном движении

1. Каждый наблюдал, как автомобили стоят на перекрёстке дорог, дожидаясь разрешающего сигнала светофора. Как только загорается зелёный свет, наиболее нетерпеливый из водителей резко трогается с места. Другой водитель начинает движение плавно. В результате оба автомобиля могут разогнаться до одной и той же скорости, но первый из них достигает необходимой скорости быстрее. В этом случае принято говорить, что первый автомобиль, набирая скорость, двигался с большим ускорением, чем второй.

Таким образом, ускорение характеризует быстроту изменения скорости. Исходя из этого, можно записать формулу ускорения по аналогии с формулой скорости.

Ускорение — векторная физическая величина, равная отношению изменения скорости Δ ко времени Δt, за которое произошло это изменение.

Эта формула позволяет рассчитать среднее ускорение. Если рассматривать малый промежуток времени, то расчёты по этой формуле дают мгновенное ускорение. В случае равноускоренного движения среднее и мгновенное ускорения равны. В дальнейшем мы будем рассматривать только движение с постоянным ускорением.

В СИ единица ускорения — метр на секунду в квадрате (м/с²).

Из формулы для расчёта ускорения тела можно выразить значение скорости в момент, когда с начала движения прошло время t.

В полученном выражении Δt = t - t₀, и если время отсчитывается с момента, когда началось движение, то t₀ = 0. Тогда формула для расчёта скорости через время t после начала движения принимает вид:

График скорости и формула перемещения

2. При прямолинейном движении, если направление оси ОХ параллельно перемещению тела, формула скорости для проекций будет иметь вид:

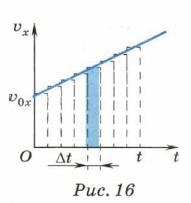
График зависимости скорости от времени, соответствующий этому уравнению, представляет собой прямую, поскольку это линейная зависимость. На рисунке 16 приведён график зависимости υ_x(t) для случая, когда значения проекций начальной скорости и ускорения положительны. По аналогии со случаем равномерного прямолинейного движения логично предположить, что проекция перемещения, совершённого телом за время t, будет равна площади фигуры, ограниченной графиком, осями координат и перпендикуляром, восставленным к графику из точки t. В данном случае эта фигура — трапеция.

Продолжение >>>