Главная >> Физика 10 класс. Мякишев

Глава 1. Кинематика точки и твёрдого тела

§ 12. Примеры решения задач по теме «Движение с постоянным ускорением

Для решения задач по этой теме необходимо правильно записывать уравнение движения и уравнение зависимости скорости от времени.

Для некоторых задач разумно строить графики зависимости проекции скорости от времени и определять перемещение по графику, что часто удобнее, чем решать задачу аналитически.

Задача 1. Ударом клюшки хоккейной шайбе сообщили скорость υ₀ = 20 м/с. Через время t = 2 с скорость шайбы, движущейся прямолинейно, стала равна 16 м/с. Определите ускорение шайбы, считая его постоянным.

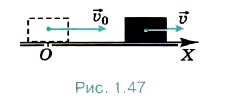
Р е ш е н и е. Выберем оси координат так, чтобы движение шайбы происходило вдоль какой-нибудь координатной оси, например вдоль оси ОХ. За положительное направление оси ОХ примем направление вектора начальной скорости (рис. 1.47). Из определения ускорения следует: а_х = (υ - υ₀)/t = -2 м/с².

Знак «—» в конечном результате означает, что вектор ускорения направлен в сторону, противоположную положительному направлению оси ОХ. Модуль же ускорения а = |а_x| = |-2 м/с²| = 2 м/с².

Задача 2. Перекрытие между первым и вторым этажами здания лифт проходил со скоростью υ0 = 4 м/с. Далее он начал тормозить и поднимался с постоянным ускорением а = 2 м/с2. Через время t = 2 с после начала торможения лифт остановился. Высота h каждого этажа равна 4 м. На какой высоте Н, считая от пола первого этажа, остановился лифт?

Р е ш е н и е. Совместим начало координат с полом первого этажа и направим ось OY вертикально вверх. Так как ускорение лифта постоянно, то его движение будет описываться кинематическим уравнением у = у₀ + υ_0yt + a_yt²/2.

Согласно условию задачи у₀ = h, υ_0y = υ₀, а_у = -а, у = Н.

Поэтому Н = h + υ₀t - at²/2; Н = 8м.

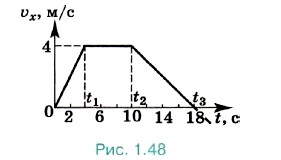
Задача 3. На рисунке 1.48 изображена зависимость проекции скорости от времени.

1) Постройте графики зависимости ускорения и перемещения от времени.

2) Определите перемещение за время, равное t₃.

3) Определите среднюю скорость движения за время, равное t₃.

Р е ш е н и е. В течение промежутка времени от 0 до материальная точка движется равноускоренно, так как скорость растёт со временем по линейному закону. Ускорение а_1х = (υ₁ - 0)/t₁ = 1 м/с².

В течение промежутка времени Δt — t₂ - t₁ материальная точка движется равномерно: υ = υ₁ = const, а₂ = 0. При t > t₂ точка движется равнозамедленно с ускорением а_3х = (0 - υ₁)/(t₃ - t₂) = -0,5 м/с².

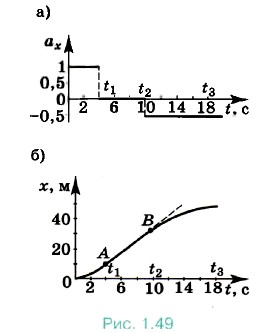
На рисунке (1.49, а) изображён график зависимости а_x от t. Зависимость x(t) в интервале 0 < t < t₁ определяется по формуле х = 0 + a_1xt²/2 и при t = t₁, х₁ = a_1xt₁²/2 = 8 м. Скорость в момент времени t₁ будет равна υ₁, и тело начнёт двигаться равномерно:

х₂ = х₁ + υ_1x(t₂ - t₁) = 32 м.

Начиная с t = t₂ тело движется равнозамедленно:

x₃ = x₂ + υ_1x(t₃ - t₂) - а_3х(t₃ - t_{2)²/2 = 48 м.}

Средняя скорость движения

υ_ср = x₃/t₃ ≈ 2,7 м/с.

График зависимости x(t) показан на рисунке (1.49, б). Кривая, изображающая зависимость x(t), состоит из трёх участков: параболы, прямой, параболы. Отметим, что парабола плавно переходит в прямую в точке А (и в точке В), так как значение мгновенной скорости определяется тангенсом угла наклона касательной к графику x(t) и в каждой точке графика должна быть единственная касательная. Перемещение также можно определить как площадь трапеции (см. рис. 1.48):

υ₃ = υ_1xt₁/2 + υ_1x(t₂ — t₁) + υ_1x(t₃ — t₂)/2 = 48 м.

Задачи для самостоятельного решения

1. Тело движется вдоль координатной оси ОХ. Направления начальной скорости и ускорения совпадают с положительным направлением оси, а их модули равны υ₀ = 4 м/с, а = 2 м/с². Определите скорость через 4 с от начала отсчёта времени.

2. В точке с координатой х₀ = 10 м тело имело скорость υ₀ = 20 м/с, направленную противоположно положительному направлению оси ОХ. Ускорение тела направлено противоположно вектору начальной скорости, а его модуль равен 10 м/с². Определите координату тела в моменты времени 1, 2, 3, 4 с от начала отсчёта.

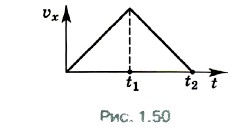
3. На рисунке 1.50 показан график зависимости проекции скорости тела от времени. Постройте график зависимости модуля перемещения от времени.