|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 13. Движение с постоянным ускорением свободного паденияЧто называют свободным падением? От чего свободно падающее тело? При изучении свободного падения тел мы будем рассматривать только такие движения, при которых ускорение свободного падения постоянно, т. е. сопротивление воздуха можно не учитывать. Эти движения будут описываться известными нам кинематическими уравнениями (1.12) и (1.14).
С движением тел, получивших начальную скорость под углом к ускорению свободного падения или под углом к горизонту, приходится встречаться довольно часто. Например: снаряд, выпущенный под углом к горизонту; ядро, которое толкнул спортсмен. Найдём траекторию тела, брошенного под углом к горизонту. Пусть из точки О брошено тело с начальной скоростью Так как ускорение свободного падения с течением времени не меняется, то движение тела в данном случае, как и любое движение с постоянным ускорением, можно описать уравнениями
Так как в начальный момент времени тело находилось в начале координат, то x0 = 0 и у0 = 0. Проекцию вектора на какую-либо ось можно выразить через модуль вектора и косинус или синус угла, который этот вектор образует с положительным направлением оси. Из рисунка 1.51 видно, что υ0x = υ0cosα, υ0y = υ0sinα, ax = 0 и ay = -g. Поэтому уравнения (1.18) и (1.19) можно записать в виде
Для построения траектории точки можно найти из уравнений (1.20) и (1.21) значения координат х и у для различных моментов времени, а затем по координатам построить точки и соединить их плавной линией.
Однако удобнее найти уравнение траектории, т. е. зависимость у от х. Чтобы получить это уравнение, нужно исключить время из уравнений (1.20) и (1.21). Из уравнения (1.20) имеем
Введём обозначения: tgα = с и
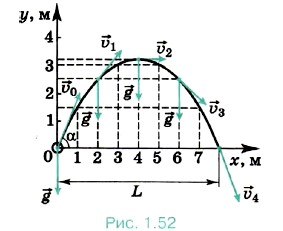
Из курса алгебры известно, что графиком функции (1.22) является парабола, ось симметрии которой — прямая, параллельная оси Y. Поскольку в данном случае b < 0, то ветви параболы направлены вниз. На рисунке 1.52 изображена парабола для случая b = -0,2 м-1 и с = 1,6. Итак, мы доказали, что если ускорение свободного падения постоянно, то тело, брошенное под углом к горизонту, движется по параболе. Теперь определим дальность и максимальную высоту полёта тела.
Дальность полёта L = (υ0cosα)tпол. (1.23) Время полёта можно определить из уравнения (1.21). При падении тела у = 0, отсюда Время подъёма Из формул (1.20) и (1.21) видно, что движение тела, брошенного под углом к горизонту, можно рассматривать как сумму двух независимых движений — равномерного движения вдоль оси ОХ и равноускоренного движения вдоль оси OY.
Теперь выясним, какой будет траектория тела, если его начальная скорость направлена горизонтально.
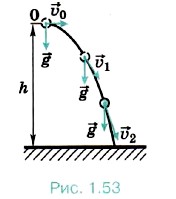
Из рисунка 1.52 видно, что, начиная с того момента, когда скорость тела горизонтальна, оно движется по ветви параболы. Следовательно, любое тело, брошенное горизонтально, будет двигаться по одной из ветвей параболы, вершина которой находится в точке бросания (рис. 1.53). Мы разобрали пример сложного движения тела. Это движение является суммой двух независимых движений — равномерного движения со скоростью
Вопросы к параграфу 1. Какую форму имеет траектория тела, брошенного под углом к горизонту? 2. При каком угле бросания дальность полёта будет максимальна? 3. Под каким углом к горизонту направлена скорость тела в наивысшей и конечной точках траектории?
|
|
|



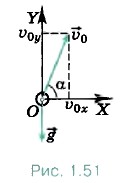
 0 под углом а к горизонту (рис. 1.51). Выберем оси координат так, чтобы векторы и
0 под углом а к горизонту (рис. 1.51). Выберем оси координат так, чтобы векторы и  были расположены в какой-либо координатной плоскости, например в плоскости XOY. Ось ОХ направим горизонтально, а ось OY — вертикально вверх. Начало координат выберем в точке бросания.
были расположены в какой-либо координатной плоскости, например в плоскости XOY. Ось ОХ направим горизонтально, а ось OY — вертикально вверх. Начало координат выберем в точке бросания.
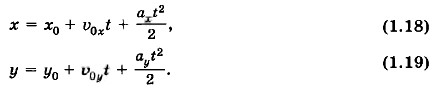

 Приведите ещё примеры ситуаций, в которых тело начинает падать с начальной скоростью, направленной под углом к горизонту.
Приведите ещё примеры ситуаций, в которых тело начинает падать с начальной скоростью, направленной под углом к горизонту.
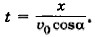 Следовательно,
Следовательно,
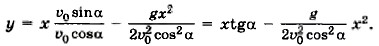
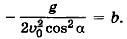 Следовательно,
Следовательно,

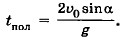 Подставив это выражение в уравнение (1.23), получим
Подставив это выражение в уравнение (1.23), получим 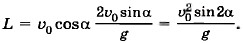
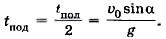 Подставив это выражение в уравнение (1.21), получим
Подставив это выражение в уравнение (1.21), получим 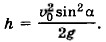
 Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте. Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струёй экран с заранее вычерченной параболой. При определённой скорости истечения воды струя будет располагаться вдоль вычерченной параболы.
Наглядное представление о траектории тела, брошенного горизонтально или под углом к горизонту, можно получить на простом опыте. Так как каждая частица воды движется по параболе, то струи воды имеют форму параболы. В этом легко убедиться, поставив за струёй экран с заранее вычерченной параболой. При определённой скорости истечения воды струя будет располагаться вдоль вычерченной параболы.