|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 23. Примеры решения задач по теме «Второй закон Ньютона»Познакомимся с задачами, для решения которых не нужно знать, как зависят силы от расстояний между взаимодействующими телами (или частями одного тела) и от их скоростей. Единственное, что нам потребуется, — это выражение для силы тяжести вблизи поверхности Земли:
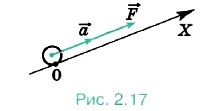
Задача 1. К центру однородного шарика массой m = 0,2 кг приложена сила F = 1,5 Н. Определите модуль и направление силы Р е ш е н и е. На шарик действуют две силы: сила
Таким образом, искомая сила может быть направлена либо так же, как сила Проанализируем последнее выражение. Если mа > F, то F1x > 0, т. е. сила F1x - 0,2 • 5Н - 1,5 Н = -0,5 Н. Следовательно, сила F1 направлена противоположно оси X (рис. 2.18).
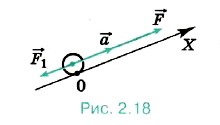
Задача 2. В результате полученного толчка брусок начал скользить вверх по наклонной плоскости из точки О с начальной скоростью υ0 = 4,4 м/с. Определите положение бруска относительно точки О через промежуток времени t1 — 2 с после начала его движения, если угол наклона плоскости к горизонту α = 30°. Трение не учитывайте. Р е ш е н и е. Поскольку требуется найти положение бруска относительно точки О, начало координат возьмём в этой точке. Ось X направим вдоль наклонной плоскости вниз, а ось Y — перпендикулярно этой плоскости вверх (рис. 2.19). При движении бруска на него действуют две силы: сила тяжести m Согласно второму закону Ньютона m
При сделанном выборе направления оси X и начала координат имеем х0 = 0 и υ0x = -υ0. Проекцию ускорения ах на ось X найдём по второму закону Ньютона. Для рассматриваемого случая mах = mgx + Nx. Учитывая, что gx = g sinα и Nx = 0, получим ах = g sinα. Таким образом,
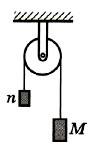
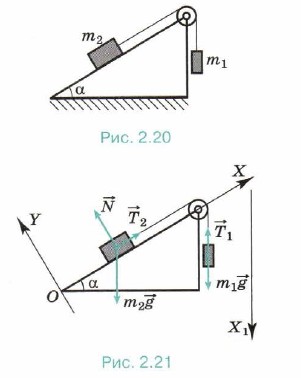
Задача 3. Два тела массами m1 = 10 г и m2 = 15 г связаны нерастяжимой и невесомой нитью, перекинутой через невесомый блок, установленный на наклонной плоскости (рис. 2.20). Плоскость образует с горизонтом угол α = 30°. Определите ускорение, с которым будут двигаться эти тела. Трение не учитывайте. Р е ш е н и е. Предположим, что тело массой m1 перетягивает. Выберем оси координат так, как показано на рисунке 2.21. В проекциях на оси Х1 и X уравнения движения тел запишем в виде m1ax1 = m1g - Т1, m2ах = Т2 — m2g sinα, |ах| =|ax1|, так как нить нерастяжима. Силы натяжения нити равны, так как нить и блок невесомы. Сложив левые и правые части уравнении, получим
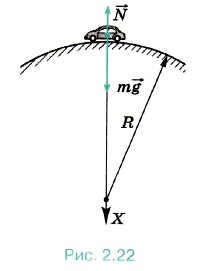
Задача 4. Автомобиль массой т = 1000 кг движется со скоростью v = 36 км/ч по выпуклому мосту, имеющему радиус кривизны R = 50 м. С какой силой F давит автомобиль на мост в его середине? С какой минимальной скоростью umin должен двигаться автомобиль для того, чтобы в верхней точке он перестал оказывать давление на мост? Р е ш е н и е. Силы, действующие на автомобиль вдоль радиуса моста, изображены на рисунке 2.22: m Отсюда F = N = m(g - υ2/R) = 7,8 кН. Сила давления на мост станет равной нулю при mυ2min/R = mg, так что υmin = 80 км/ч. При скорости, превышающей υmin, автомобиль оторвётся от поверхности моста.
Задачи для самостоятельного решения 1. К центру шара приложена сила 2. На полу лифта находится тело массой 50 кг. Лифт поднимается так, что за 3 с его скорость изменяется от 8 до 2 м/с. Определите силу давления тела на пол лифта. 3. Тепловоз на горизонтальном участке пути длиной 600 м развивает постоянную силу тяги 147 кН. Скорость поезда возрастает при этом от 36 до 54 км/ч. Определите силу сопротивления движению, считая её постоянной. Масса поезда 1000 т. 4. Жёсткий стержень длиной 1 м с прикреплённым к нему шариком массой 100 г вращается равномерно в вертикальной плоскости. Определите модуль и направление силы, с которой стержень действует на шарик в верхней точке, при скоростях шарика 2 м/с и 4 м/с. 5. Два груза массами 2 кг и 4 кг, связанные нерастяжимой нитью, поднимают вертикально силой 84 Н, приложенной к первому грузу. Определите ускорение, с которым движутся грузы, и силу натяжения нити.
|
|
|



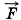 τ = m
τ = m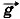 .
.
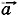 =
= 
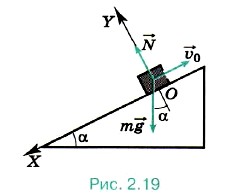
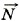 наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.
наклонной плоскости, перпендикулярная последней. Эту силу иногда называют силой нормальной реакции. Она всегда перпендикулярна поверхности, на которой находится тело.
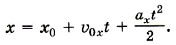
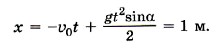
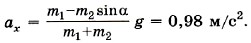 Так как ах > 0, то движение тел происходит в выбранном направлении.
Так как ах > 0, то движение тел происходит в выбранном направлении.