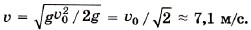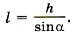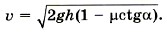|
|
|
|
|
Глава 5. Закон сохранения энергии § 42. Примеры решения задач по теме «Кинетическая энергия и её изменение»Очень часто для решения задач о движении тела, скорость которого изменяется, удобно пользоваться теоремой об изменении кинетической энергии. Такой способ позволяет решать задачи и в том случае, когда силы, действующие на тело, являются переменными. Очевидно, что решение подобных задач на основании второго закона Ньютона затруднено тем, что движение происходит с переменным ускорением. Задача 1. Шофёр выключает двигатель и начинает тормозить, когда видит, что впереди меняют асфальт и дорога покрыта песком. Начальная скорость автомобиля 90 км/ч. Шофёр нажал на тормоз на расстоянии 60 м от границы между асфальтом и песком. Определите коэффициент трения колёс автомобиля о дорогу, покрытую песком, если машина до остановки проехала по ней 2,5 м. Коэффициент трения колёс машины об асфальт μ1 = 0,5.
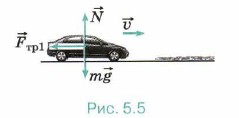
Р е ш е н и е. Согласно теореме об изменении кинетической энергии изменение кинетической энергии автомобиля равно алгебраической сумме работ всех сил, действующих на него. На автомобиль действуют (рис. 5.5) сила тяжести m Силы тяжести и нормальной реакции опоры перпендикулярны перемещению, поэтому работы их на данном перемещении равны нулю. Тогда 0 - mυ2/2 = -Fтр1s1 - Fтp2s2 = -(μ1s1 + μ2s2)N. Очевидно, что N = mg. Подставив N в уравнение, получим mυ2/2 = (μ1s1 + μ2s2)mg. Окончательно
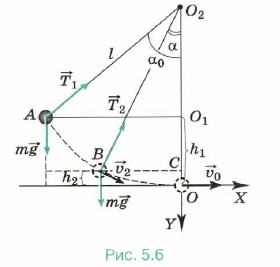
Задача 2. Маятник, представляющий собой маленький шарик, подвешенный на тонкой нити длиной 1 м, отклонили так, что нить стала составлять с вертикалью угол 60°. Затем шарик отпустили. Определите скорость шарика в тот момент, когда угол отклонения нити равен 30° и когда шарик проходит положение равновесия. Р е ш е н и е. На шарик во время движения действуют две силы — сила тяжести и сила натяжения (рис. 5.6). Изменение кинетической энергии шарика при перемещении из точки А в точку В равно: mυ22/2 - 0 = Ат + Ан. (1) Работа силы натяжения равна нулю, так как она всё время перпендикулярна перемещению. На основании закона о независимости движений движение шарика можно рассматривать как сумму двух движений: по оси ОХ и по оси OY. Работа силы тяжести при перемещении шарика вдоль оси ОХ равна нулю, так как сила тяжести перпендикулярна перемещению вдоль этой оси. Работа силы тяжести при перемещении вдоль оси OY равна Ат = mgΔy, где Δу = h1 - h2. Из треугольника АO2O1 получим O1O2 = lcosα0, тогда h1 = l - O1O2 = l(1 - cosα0), а из треугольника ВO2С получим O2С = lcosα, h2 = l - O2С = l(1 - cosα). Окончательно h1 - h2 = l(cosα - cosα0). Работа силы тяжести равна Ат = mgl(cosα - cosα0). Подставив найденное выражение для работы в уравнение (1), получим m22/2 = mgl(cosα - cosα0). Скорость в точке В: Перемещение шарика вдоль оси OY при движении из точки А в точку О равно h1. Тогда скорость шарика в точке О: Задача 3. Тело брошено вертикально вверх со скоростью υ0 = 10 м/с. Определите наибольшую высоту подъёма hmах, а также скорость тела на высоте, равной hmax/2. Силой сопротивления воздуха можно пренебречь. Р е ш е н и е. Изменение кинетической энергии тела при подъёме на максимальную высоту равно работе силы тяжести: 0 - mυ20/2 = -mghmax. Из этого уравнения сразу же получаем выражение для максимальной высоты подъёма: hmах = υ20/2g = 5 м. Скорость тела на некоторой высоте при падении равна его скорости на той же высоте при подъёме. Определим скорость тела при падении с максимальной высоты. Согласно теореме об изменении кинетической энергии mυ2/2 - 0 = mgh = mghmax/2. (Сила тяжести при спуске совершает положительную работу.) Тогда для скорости получаем формулу
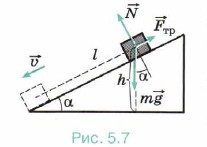
Задача 4. Груз тянут вверх по наклонной плоскости с углом а у основания. На высоте h верёвка обрывается. Определите скорость груза у основания плоскости. Коэффициент трения груза о плоскость равен μ. Р е ш е н и е. На груз действуют силы тяжести, нормальной реакции опоры и трения (рис. 5.7). Изменение кинетической энергии при соскальзывании груза равно: mυ2/2 - 0 = Ат + Атр. Работа силы нормальной реакции опоры равна нулю, так как эта сила перпендикулярна перемещению. Как видно из рисунка, работа силы тяжести равна Ат = mgl sina = mgh. Сила трения Fтр = μN = μmgcosα. Работа силы трения Атр = -μmg cosα. Длина пути Тогда Атр = -μmgh cosα/sinα = -μmghctgα. Подставив найденные выражения для работ сил тяжести и трения в уравнение (1), получим mυ2/2 = mgh - μmghctgα = mgh(1 - μctgα). Тогда для скорости получим выражение Задачи для самостоятельного решения 1. Мяч массой 1 кг падает с высоты 2 м. Определите изменение кинетической энергии мяча на первой и второй половинах пути. 2. Человек сначала несёт груз массой 4 кг до шкафа, а затем ставит его на шкаф, подняв груз на высоту 1 м. Определите работу силы тяжести, действующей на груз при его перемещении. 3. Скорость тела массой 2 кг изменяется согласно уравнению υх = 5 + 4t + 2t2 . Определите работу сил, действующих на тело в течение первых четырёх секунд.
|
|
|



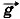 сила нормальной реакции опоры
сила нормальной реакции опоры 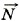 , сила трения, причём на первом участке пути сила трения равна Fтp1 = μ1N, а на втором — Fтp2 = μ2N.
, сила трения, причём на первом участке пути сила трения равна Fтp1 = μ1N, а на втором — Fтp2 = μ2N.
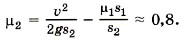
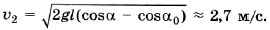
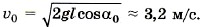
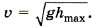 С учётом выражения для hmax окончательно получим
С учётом выражения для hmax окончательно получим