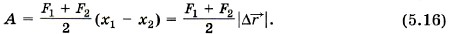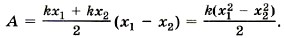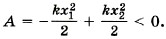|
|
|
|
|
Глава 5. Закон сохранения энергии § 43. Работа силы тяжести и силы упругости. Консервативные силыПо какой формуле можно вычислить работу силы? Что общего между работой силы тяжести и силы упругости?
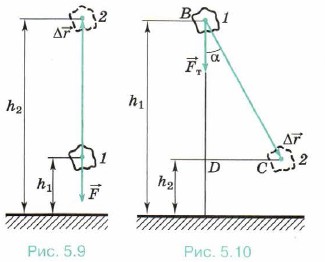
Работа силы тяжести. Вычислим работу силы тяжести при падении тела (например, камня) вертикально вниз. В начальный момент времени тело находилось на высоте hx над поверхностью Земли, а в конечный момент времени — на высоте h2 (рис. 5.8). Модуль перемещения тела |Δ Направления векторов силы тяжести А = | Пусть теперь тело бросили вертикально вверх из точки, расположенной на высоте h1 над поверхностью Земли, и оно достигло высоты h2 (рис. 5.9). Векторы А = |
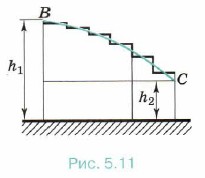
Если же тело перемещается по прямой так, что направление перемещения составляет угол а с направлением силы тяжести (рис. 5.10), то работа силы тяжести равна: А = | Из прямоугольного треугольника BCD видно, что |BC|cosα = BD = h1 — h2. Следовательно, А = mg(h1 - h2) = mgh1 - mgh2. (5.14) Это выражение совпадает с выражением (5.12). Формулы (5.12), (5.13), (5.14) дают возможность подметить важную закономерность. При прямолинейном движении тела работа силы тяжести в каждом случае равна разности двух значений величины, зависящей от положений тела, определяемых высотами h1 и h2 над поверхностью Земли.
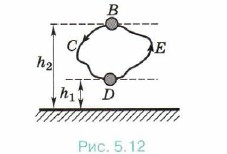
Более того, работа силы тяжести при перемещении тела массой т из одного положения в другое не зависит от формы траектории, по которой движется тело. Действительно, если тело перемещается вдоль кривой ВС (рис. 5.11), то, представив эту кривую в виде ступенчатой линии, состоящей из вертикальных и горизонтальных участков малой длины, увидим, что на горизонтальных участках работа силы тяжести равна нулю, так как сила перпендикулярна перемещению, а сумма работ на вертикальных участках равна работе, которую совершила бы сила тяжести при перемещении тела по вертикальному отрезку длиной h1 - h2. Таким образом, работа силы тяжести при перемещении вдоль кривой ВС равна: А = mgh1 - mgh2.
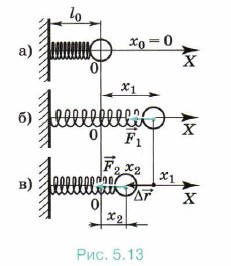
Определим работу А при перемещении тела по замкнутому контуру, например по контуру BCDEB (рис. 5.12). Работа А1 силы тяжести при перемещении тела из точки В в точку D по траектории BCD: А1 = mg(h2 - h1), по траектории DEB: А2 = mg(h1 - h2). Тогда суммарная работа А = А1 + А2 = mg(h2 - h1) + mg(h1 - h2) = 0.
Итак, работа силы тяжести не зависит от формы траектории тела; она определяется лишь начальным и конечным положениями тела. При перемещении тела по замкнутой траектории работа силы тяжести равна нулю.
Работа силы упругости. Вычислим работу, которую совершает сила упругости при перемещении некоторого груза. На рисунке 5.13, а показана пружина, у которой один конец закреплён неподвижно, а к другому концу прикреплён шар. Совместим начало координат с центром шара, тогда координата шара будет равна удлинению пружины. Если пружина растянута, то она действует на шар с силой |Δ
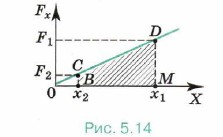
Мы рассматриваем случай, когда направления силы упругости и перемещения тела совпадают. Для вычисления работы переменной силы упругости воспользуемся графиком зависимости модуля силы упругости от координаты шара (рис. 5.14). В § 40 мы показали, что работа может быть определена по графику зависимости Fx от х и что эта работа численно равна площади заштрихованной фигуры (см. рис. 5.3, б). В нашем примере работа силы упругости на перемещении х1 - х2 точки её приложения численно равна площади трапеции BCDM. Следовательно,
Согласно закону Гука значения сил упругости F1 = kx1 и F2 = kx2. Подставляя эти выражения в уравнение (5.16) и учитывая, что |Δ
Или окончательно
Работа силы упругости при растяжении пружины, т. е. когда направление силы противоположно перемещению тела:
Во всех случаях движения тела под действием силы упругости мы пришли бы к той же формуле (5.17) для работы, т. е. работа силы упругости зависит лишь от удлинения или сжатия пружины в начальном и конечном состояниях. Таким образом, работа силы упругости не зависит от формы траектории и, так же как и сила тяжести, сила упругости является консервативной.
Вопросы к параграфу 1. Чему равна работа силы тяжести и силы упругости при перемещении тела по замкнутой траектории? 2. Какие силы называют консервативными? Каково их общее свойство?
|
|
|



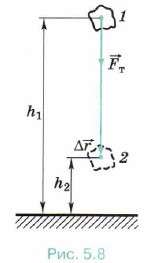
 | = h1 - h2.
| = h1 - h2.
 T и перемещения Δ
T и перемещения Δ Предположите, что тело перемещается между точками 1 и 2 (см. рис. 5.10) по ломаной линии. Покажите, что работа силы тяжести и в этом случае определяется выражением (5.13).
Предположите, что тело перемещается между точками 1 и 2 (см. рис. 5.10) по ломаной линии. Покажите, что работа силы тяжести и в этом случае определяется выражением (5.13).