|
|
|
|
|
Глава 1. Кинематика точки и твёрдого тела § 5. Примеры решения задач по теме «Равномерное прямолинейное движение»При решении задач по данной теме необходимо прежде всего выбрать тело отсчёта и связать с ним систему координат. В данном случае движение происходит по прямой, поэтому для его описания достаточна одна ось, например ось ОХ. Выбрав начало отсчёта, записываем уравнения движения. Задача I. Определите модуль и направление скорости точки, если при равномерном движении вдоль оси ОХ её координата за время t1 = 4 с изменилась от х1 = 5 м до х2 = -3 м. Р е ш е н и е. Модуль и направление вектора можно найти по его проекциям на оси координат. Так как точка движется равномерно, то проекцию её скорости на ось ОХ найдём по формуле
Отрицательный знак проекции скорости означает, что скорость точки направлена противоположно положительному направлению оси ОХ. Модуль скорости υ = |υх| = |-2 м/с| = 2 м/с.
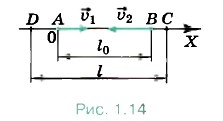
Задача 2. Из пунктов А и В, расстояние между которыми вдоль прямого шоссе l0 = 20 км, одновременно навстречу друг другу начали равномерно двигаться два автомобиля. Скорость первого автомобиля υ1 = 50 км/ч, а скорость второго автомобиля υ2 = 60 км/ч. Определите положение автомобилей относительно пункта А спустя время t = 0,5 ч после начала движения и расстояние I между автомобилями в этот момент времени. Определите пути s1 и s2, пройденные каждым автомобилем за время t. Р е ш е н и е. Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.14). Движение автомобилей будет описываться уравнениями x1 = х01 + υ1xt, x2 = х02 + υ2xt. Так как первый автомобиль движется в положительном направлении оси ОХ, а второй — в отрицательном, то υ1x = υ1, υ2x = —υ2. В соответствии с выбором начала координат х01 = 0, х02 = l0. Поэтому спустя время t x1 = υ1t = 50 км/ч • 0,5 ч = 25 км; х2 = l0 — υ2t = 20 км - 60 км/ч • 0,5 ч = -10 км. Первый автомобиль будет находиться в точке С на расстоянии 25 км от пункта А справа, а второй — в точке D на расстоянии 10 км слева. Расстояние между автомобилями будет равно модулю разности их координат: l = |х2 - x1| = |—10 км - 25 км| = 35 км. Пройденные пути равны: s1 = υ1t = 50 км/ч • 0,5 ч = 25 км, s2 = υ2t = 60 км/ч • 0,5 ч = 30 км.
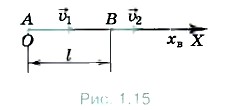
Задача 3. Из пункта А в пункт В выезжает первый автомобиль со скоростью υ1 Спустя время t0 из пункта В в том же направлении со скоростью υ2 выезжает второй автомобиль. Расстояние между пунктами A и В равно l. Определите координату места встречи автомобилей относительно пункта В и время от момента отправления первого автомобиля, через которое они встретятся. Р е ш е н и е. Примем пункт А за начало координат и направим координатную ось ОХ в сторону пункта В (рис. 1.15). Движение автомобилей будет описываться уравнениями x1 = υ1t, х2 = l + υ2( t - t0). В момент встречи координаты автомобилей равны: х1 = х2 = хв. Тогда υ1tв = l + υ2( tв - t0) и время до встречи Очевидно, что решение имеет смысл при υ1 > υ2 и l > υ2t0 или при υ1 < υ2 и l < υ2t0. Координата места встречи
Задача 4. На рисунке 1.16 представлены графики зависимости координат точек от времени. Определите по графикам: 1) скорости точек; 2) через какое время после начала движения они встретятся; 3) пути, пройденные точками до встречи. Напишите уравнения движения точек. Р е ш е н и е. За время, равное 4 с, изменение координаты первой точки: Δx1 = 4 - 2 (м) = 2 м, второй точки: Δх2 = 4 - 0 (м) = 4 м. 1) Скорости точек определим по формуле 2) Время встречи — это момент времени, когда координаты точек равны. Очевидно, что tв = 4 с. 3) Пути, пройденные точками, равны их перемещениям и равны изменениям их координат за время до встречи: s1 = Δх1= 2 м, s2 = Δх2 = 4 м. Уравнения движения для обеих точек имеют вид х = х0 + υxt, где х0 = x01 = 2 м, υ1x = 0,5 м/с — для первой точки; х0 = х02 = 0, υ2x = 1 м/с — для второй точки. Задачи для самостоятельного решения1. При равномерном движении точки по прямой, совпадающей с осью ОХ, координата точки изменилась от 8 до -8 м. Определите время, в течение которого произошло изменение координаты, если модуль скорости равен 4 м/с. Какой путь прошла точка за это время?
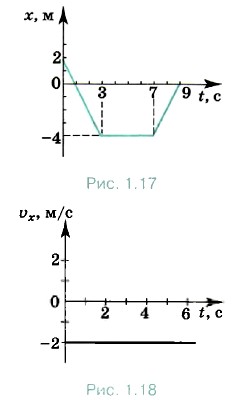
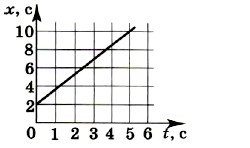
2. На рисунке 1.17 изображён график зависимости координаты от времени для точки, движущейся вдоль оси ОХ. Опишите движение точки в интервалах времени от 0 до 3 с, от 3 до 7 с и от 7 до 9 с. Постройте графики модуля и проекции скорости в зависимости от времени. Начертите график зависимости пути от времени. 3. На рисунке 1.18 изображён график зависимости проекции скорости от времени при движении точки вдоль оси ОХ. Чему равен модуль скорости точки? В каком направлении оси ОХ она движется? Чему равно изменение координаты за 6 с, и какой путь пройден точкой за это время? Постройте график зависимости координаты от времени, если x0 = 6 м. Постройте график зависимости пути от времени. В чём различие графиков? 4. Из пунктов, отстоящих друг от друга на расстоянии 90 км, одновременно выехали два автобуса со скоростями 60 и 30 км/ч, направленными вдоль прямого шоссе, соединяющего эти пункты. Через сколько времени автобусы встретятся? Рассмотрите все возможные случаи.
|
|
|



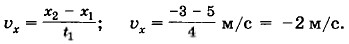
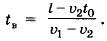
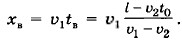
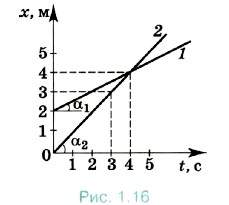
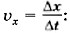 υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.
υ1x = 0,5 м/с; υ2x = 1 м/с. Заметим, что эти же значения можно было получить по графикам, определив тангенсы углов наклона прямых к оси времени: скорость υ1x численно равна tgα1, а скорость υ2x численно равна tgα2.