|
|
|
|
|
Глава 9. Молекулярно-кинетическая теория идеального газа § 60. Определение температуры. Энергия теплового движения молекул (окончание)Постоянная Больцмана. Определим коэффициент k в формуле (9.13) так, чтобы изменение температуры на один кельвин (1 К) было равно изменению температуры на один градус по шкале Цельсия (1 °С). Мы знаем значения величины Θ при 0 °С и 100 °С (см. формулы (9.9) и (9.11)). Обозначим абсолютную температуру при 0 °С через Т1, а при 100 °С через Т2. Тогда согласно формуле (9.12) Θ100 - Θ0 = k(T2 -T1), Θ100 - Θ0 = k • 100 K = (5,14 - 3,76) • 10-21 Дж. Отсюда
Это одна из наиболее важных постоянных в молекулярно-кинетической теории. Зная постоянную Больцмана, можно найти значение абсолютного нуля по шкале Цельсия. Для этого найдём сначала значение абсолютной температуры, соответствующее 0 °С. Так как при 0 °С kT1 = 3,76 • 10-21 Дж, то
Один кельвин и один градус шкалы Цельсия совпадают. Поэтому любое значение абсолютной температуры Т будет на 273 градуса выше соответствующей температуры t по Цельсию: Т (К) = (f + 273) (°С). (9.15)
На рисунке 9.5 для сравнения изображены абсолютная шкала и шкала Цельсия. Абсолютному нулю соответствует температура t = -273 °С.
Отметим важнейший факт: абсолютный нуль температуры недостижим! Температура — мера средней кинетической энергии молекул. Из основного уравнения молекулярно-кинетической теории (9.8) и определения температуры (9.13) вытекает важнейшее следствие:
Докажем это. Из уравнений (9.7) и (9.13) следует, что
Чем выше температура, тем быстрее движутся молекулы. Таким образом, выдвинутая ранее догадка о связи температуры со средней скоростью молекул получила надёжное обоснование. Соотношение (9.16) между температурой и средней кинетической энергией поступательного движения молекул установлено для идеальных газов. Однако оно оказывается справедливым для любых веществ, у которых движение атомов или молекул подчиняется законам механики Ньютона. Оно верно для жидкостей, а также и для твёрдых тел, где атомы могут лишь колебаться возле положений равновесия в узлах кристаллической решётки. При приближении температуры к абсолютному нулю энергия теплового движения молекул приближается к нулю, т. е. прекращается поступательное тепловое движение молекул.
Зависимость давления газа от концентрации его молекул и температуры. Учитывая, что
Из формулы (9.17) вытекает, что при одинаковых давлениях и температурах концентрация молекул у всех газов одна и та же. Отсюда следует закон Авогадро, известный вам из курса химии.
Вопросы к параграфу 1. На каком основании можно предполагать существование связи между температурой и кинетической энергией молекул? 2. Как связаны объём, давление и число молекул различных газов в состоянии теплового равновесия? 3. Чему равен абсолютный нуль температуры по шкале Цельсия? 4. Какие преимущества имеет абсолютная шкала температур по сравнению со шкалой Цельсия? 5. Каков физический смысл постоянной Больцмана? Можно ли её определить теоретически, не обращаясь к эксперименту? 6. Как зависит от температуры средняя кинетическая энергия поступательного движения молекул газа? 7. Почему концентрация молекул всех газов одна и та же при одинаковых давлениях и температурах? 8. Как зависит средняя кинетическая энергия поступательного движения молекул от их массы?
<<< К началу параграфа Следующая страница >>>
|
|
|



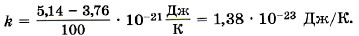

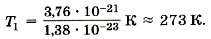
 Следует ли из фразы «Один кельвин и один градус шкалы Цельсия совпадают», что 27 °С = 27 К?
Следует ли из фразы «Один кельвин и один градус шкалы Цельсия совпадают», что 27 °С = 27 К?
 В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32 °F, а точка кипения 212 °Е Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) = 5/9 (t(°F) - 32).
В США используется шкала Фаренгейта. Точка замерзания воды по этой шкале 32 °F, а точка кипения 212 °Е Пересчёт температуры из шкалы Фаренгейта в шкалу Цельсия производится по формуле t(°C) = 5/9 (t(°F) - 32).
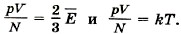 Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:
Отсюда вытекает связь между средней кинетической энергией поступательного движения молекулы и температурой:

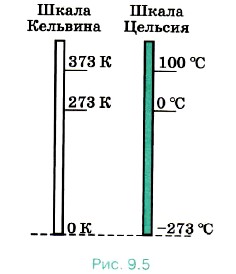
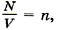 из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:
из формулы (9.13) получим выражение, показывающее зависимость давления газа от концентрации молекул и температуры:

