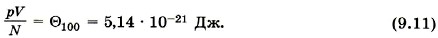|
|
|
|
|
Глава 9. Молекулярно-кинетическая теория идеального газа § 60. Определение температуры. Энергия теплового движения молекулКакие макропараметры используют для описания состояния газа? Справедливо ли утверждение: «Чем быстрее движутся молекулы газа, тем выше его температура»? Средняя кинетическая энергия молекул газа при тепловом равновесии. Возьмём сосуд, разделённый пополам перегородкой, проводящей тепло. В одну половину сосуда поместим кислород, а в другую — водород, имеющие разную температуру. Спустя некоторое время газы будут иметь одинаковую температуру, не зависящую от рода газа, т. е. будут находиться в состоянии теплового равновесия. Для определения температуры выясним, какая физическая величина в молекулярно-кинетической теории обладает таким же свойством. Из курса физики основной школы известно, что, чем быстрее движутся молекулы, тем выше температура тела. При нагревании газа в замкнутом сосуде давление газа возрастает. Согласно же основному уравнению молекулярно-кинетической теории (9.7) давление газа р прямо пропорционально средней кинетической энергии поступательного движения молекул: Так как концентрация молекул газа При тепловом равновесии, если давление и объём газа массой m постоянны и известны, то средняя кинетическая энергия молекул газа должна иметь строго определённое значение, как и температура. Можно предположить, что
Конечно, это пока только предположение. Его нужно экспериментально проверить. Практически такую проверку произвести непосредственно невозможно, так как измерить среднюю кинетическую энергию молекул очень трудно. Но с помощью основного уравнения молекулярно-кинетической теории её можно выразить через макроскопические параметры:
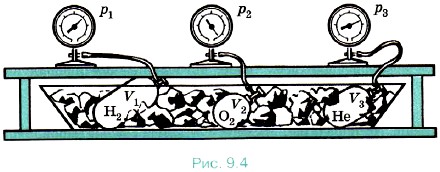
Если кинетическая энергия действительно одинакова для всех газов в состоянии теплового равновесия, то и значение давления р должно быть тоже одинаково для всех газов при Газы в состоянии теплового равновесия. Рассмотрим следующий опыт. Возьмём несколько сосудов, заполненных различными газами, например водородом, гелием и кислородом. Сосуды имеют определённые объёмы и снабжены манометрами. Это позволяет измерить давление в каждом сосуде. Массы газов известны, тем самым известно число молекул в каждом сосуде.
Приведём газы в состояние теплового равновесия. Для этого поместим их в тающий лёд и подождём, пока не установится тепловое равновесие и давление газов перестанет меняться (рис. 9.4). После этого можно утверждать, что все газы имеют одинаковую температуру 0 °С. Давления газов р, их объёмы V и число молекул N различны. Найдём отношение
Если взять водород в объёме, равном kVH2, то и число молекул будет равно kNA и отношение Такое же значение отношения произведения давления газа на его объём к числу молекул получается и для всех других газов при температуре тающего льда. Обозначим это отношение через Θ0. Тогда
Таким образом, наше предположение оказалось верным.
Если же сосуды с газами поместить в кипящую воду при нормальном атмосферном давлении, то согласно эксперименту отношение
Определение температуры. Можно, следовательно, утверждать, что величина Θ растёт с повышением температуры. Более того, Θ ни от чего, кроме температуры, не зависит. Ведь для идеальных газов Θ не зависит ни от рода газа, ни от его объёма или давления, а также от числа частиц в сосуде. Этот опытный факт позволяет рассматривать величину Θ как естественную меру температуры, как параметр газа, определяемый через другие макроскопические параметры газа. В принципе можно было бы считать температурой и саму величину Θ и измерять температуру в энергетических единицах — джоулях. Однако, во-первых, это неудобно для практического использования (температуре 100 °С соответствовало бы очень малое значение — порядка 10-21 Дж), а во-вторых, и это главное, уже давно
Абсолютная температура. Вместо температуры Θ, выражаемой в энергетических единицах, введём температуру, выражаемую в привычных для нас градусах. Будем считать величину Θ прямо пропорциональной температуре Т, измеряемой в градусах: Θ = kТ, (9.12) где k — коэффициент пропорциональности.
Такое название, как мы сейчас увидим, имеет достаточные основания. Учитывая определение (9.12), получим
По этой формуле вводится температурная шкала (в градусах), не зависящая от вещества, используемого для измерения температуры. Температура, определяемая формулой (9.13), очевидно, не может быть отрицательной, так как все величины, стоящие в левой части этой формулы, заведомо положительны. Следовательно, наименьшим возможным значением температуры Т является значение Т = 0, если давление р или объём V равны нулю.
Это самая низкая температура в природе, та «наибольшая или последняя степень холода», существование которой предсказывал Ломоносов. Английский учёный У. Томсон (лорд Кельвин) (1824—1907) ввёл абсолютную шкалу температур. Нулевая температура по абсолютной шкале (её называют также шкалой Кельвина) соответствует абсолютному нулю, а каждая единица температуры по этой шкале равна градусу по шкале Цельсия.
|
|
|



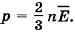
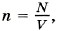 то из уравнения (9.7) получаем
то из уравнения (9.7) получаем 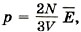 или
или 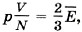 или, согласно формуле (8.8),
или, согласно формуле (8.8), 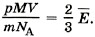

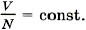
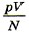 для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объём VH2 = 0,1 м3 , то при температуре 0 °С давление оказывается равным рН2 = 2,265 • 104 Па. Отсюда
для водорода. Если, к примеру, водород, количество вещества которого равно 1 моль, занимает объём VH2 = 0,1 м3 , то при температуре 0 °С давление оказывается равным рН2 = 2,265 • 104 Па. Отсюда
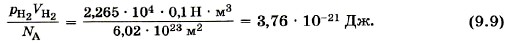
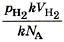 останется равным 3,76 • 10-21 Дж.
останется равным 3,76 • 10-21 Дж.

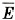 , а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение
, а также давление р в состоянии теплового равновесия одинаковы для всех газов, если их объёмы и количества вещества одинаковы или если отношение 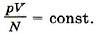
 Соотношение (9.10) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение
Соотношение (9.10) не является абсолютно точным. При давлениях в сотни атмосфер, когда газы становятся весьма плотными, отношение 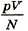 перестаёт быть строго определённым, не зависящим от занимаемых газами объёмов. Оно выполняется для газов, когда их можно считать идеальными.
перестаёт быть строго определённым, не зависящим от занимаемых газами объёмов. Оно выполняется для газов, когда их можно считать идеальными.