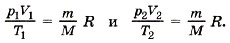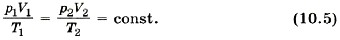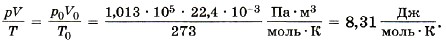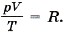Главная >> Физика 10 класс. Мякишев

Глава 10. Уравнение состояния идеального газа. Газовые законы

§ 63. Уравнение состояния идеального газа

В этой главе вы не встретите принципиально новых сведений о газах. Речь пойдёт о следствиях, которые можно извлечь из понятия температуры и других макроскопических параметров. Основное уравнение молекулярнокинетической теории газов вплотную приблизило нас к установлению связей между этими параметрами.

Как можно рассчитать массу воздуха в кабинете физики?

Какие параметры воздуха будут необходимы для определения этой массы?

Мы детально рассмотрели поведение идеального газа с точки зрения молекулярно-кинетической теории. Была определена зависимость давления газа от концентрации его молекул и температуры (см. формулу (9.17)).

На основе этой зависимости можно получить уравнение, связывающее все три макроскопических параметра р, V и Т, характеризующие состояние идеального газа данной массы.

Заметим, что формулой (9.17) можно пользоваться только до давления порядка 10 атм.

Запомни Уравнение, связывающее три макроскопических параметра р, V и Т, называют уравнением состояния идеального газа.

Подставим в уравнение р = nkT выражение для концентрации молекул газа. Учитывая формулу (8.8), концентрацию газа можно записать так:

где N_A — постоянная Авогадро, m — масса газа, М — его молярная масса. После подстановки формулы (10.1) в выражение (9.17) будем иметь

Запомни Произведение постоянной Больцмана k и постоянной Авогадро NA называют универсальной (молярной) газовой постоянной и обозначают буквой R: R = kNA = 1,38 • 10-23 Дж/К • 6,02 • 1023 1/моль = 8,31 Дж/(моль • К). (10.3)

Подставляя в уравнение (10.2) вместо kN_A универсальную газовую постоянную R, получаем

Важно уравнение состояния идеального газа произвольной массы

Единственная величина в этом уравнении, зависящая от рода газа, — это его молярная масса.

Из уравнения состояния вытекает связь между давлением, объёмом и температурой идеального газа, который может находиться в двух любых состояниях.

Если индексом 1 обозначить параметры, относящиеся к первому состоянию, а индексом 2 — параметры, относящиеся ко второму состоянию, то согласно уравнению (10.4) для газа данной массы

Правые части этих уравнений одинаковы, следовательно, должны быть равны и их левые части:

Известно, что один моль любого газа при нормальных условиях (р₀ = 1 атм = 1,013 • 10⁵ Па, t = 0 °С или Т = 273 К) занимает объём 22,4 л. Для одного моля газа, согласно соотношению (10.5), запишем:

Мы получили значение универсальной газовой постоянной R.

Таким образом, для одного моля любого газа

Запомни Уравнение состояния в форме (10.4) было впервые получено великим русским учёным Д. И. Менделеевым. Его называют уравнением Менделеева—Клапейрона. Уравнение состояния в форме (10.5) называется уравнением Клапейрона и представляет собой одну из форм записи уравнения состояния.

Б. Клапейрон в течение 10 лет работал в России профессором в институте путей сообщения. Вернувшись во Францию, участвовал в постройке многих железных дорог и составил множество проектов по постройке мостов и дорог. Его имя внесено в список величайших учёных Франции, помещённый на первом этаже Эйфелевой башни.

Уравнение состояния не надо выводить каждый раз, его надо запомнить. Неплохо было бы помнить и значение универсальной газовой постоянной:

R = 8,31 Дж/(моль • К).

До сих пор мы говорили о давлении идеального газа. Но в природе и в технике мы очень часто имеем дело со смесью нескольких газов, которые при определённых условиях можно считать идеальными.

Самый важный пример смеси газов — воздух, являющийся смесью азота, кислорода, аргона, углекислого газа и других газов. Чему же равно давление смеси газов?

Для смеси газов справедлив закон Дальтона.

Закон Дальтона Давление смеси химически невзаимодействующих газов равно сумме (ЦЩй их парциальных давлений: p = p1 + p2 + ... + pi + ... . где рi — парциальное давление i-й компоненты смеси.

Ключевые слова для поиска информации по теме параграфа. Уравнение состояния. Универсальная газовая постоянная

Вопросы к параграфу

1. Что называют уравнением состояния?

2. Какая форма уравнения состояния содержит больше информации: уравнение Клапейрона или уравнение Менделеева — Клапейрона?

3. Почему газовая постоянная R называется универсальной?

4. Сформулируйте закон Дальтона.

Образцы заданий ЕГЭ A1. Уравнение Менделеева—Клапейрона 1) связывает между собой макропараметры газа 2) связывает между собой микропараметры газа 3) связывает макропараметры газа с его микропараметрами 4) не связано ни с микропараметрами, ни с макропараметрами A2.Кислород находится в сосуде вместимостью 0,4 м3 под давлением 8,3 • 105 Па и при температуре 320 К. Чему равна масса кислорода? Молярная масса кислорода 0,032 кг/моль. 1) 2 кг       2) 0,4 кг       3) 4 кг       4) 2 • 10-23 кг A3.Азот массой 0,3 кг при температуре 280 К оказывает давление на стенки сосуда, равное 8,3 • 104 Па. Чему равен объём газа? Молярная масса азота 0,028 кг/моль. 1) 0,3 м3       2) 3,3 м3       3) 0,6 м3       4) 60 м3 A4.В сосуде находится жидкий азот N2 массой 10 кг. Какой объём займёт этот газ при нормальных условиях (273 К; 100 кПа)? Молярная масса азота 0,028 кг/моль. 1) 4,05 м3       2) 8,1 м3       3) 16,2 м3       4) 24,3 м3 A5.В баллоне вместимостью 1,66 м3 находится азот массой 2 кг при давлении 100 кПа. Чему равна температура этого газа? Молярная масса азота 0,028 кг/моль. 1) 280 °С       2) 140 °С       3) 7 °С       4) -13 °С