|
|
|
|
|
Глава 13. Основы термодинамики § 74. Работа в термодинамикеВ результате каких процессов может изменяться внутренняя энергия? Как определяется работа в механике? Работа в механике и термодинамике. В механике работа определяется как произведение модуля силы, модуля перемещения точки её приложения и косинуса угла между векторами силы и перемещения. При действии силы на движущееся тело работа этой силы равна изменению его кинетической энергии. Работа в термодинамике определяется так же, как и в механике, но она равна не изменению кинетической энергии тела, а изменению его внутренней энергии. Изменение внутренней энергии при совершении работы. Почему при сжатии или расширении тела меняется его внутренняя энергия? Почему, в частности, нагревается воздух при накачивании велосипедной шины? Причина изменения температуры газа в процессе его сжатия состоит в следующем:
Так, при движении навстречу молекулам газа поршень во время столкновений передаёт им часть своей механической энергии, в результате чего увеличивается внутренняя энергия газа и он нагревается. Поршень действует подобно футболисту, встречающему летящий на него мяч ударом ноги. Нога футболиста сообщает мячу скорость, значительно большую той, которой он обладал до удара. И наоборот, если газ расширяется, то после столкновения с удаляющимся поршнем скорости молекул уменьшаются, в результате чего газ охлаждается. Так же действует и футболист, для того чтобы уменьшить скорость летящего мяча или остановить его, — нога футболиста движется от мяча, как бы уступая ему дорогу.
Вычислим работу силы
Модуль силы, действующей со стороны газа на поршень, равен F' = pS, где р — давление газа, а S — площадь поверхности поршня. При подъёме поршня на малое расстояние Δh = h2 - h1 работа газа равна: А' = F'Δh = pS(h2 - h1) = p(Sh2 - Sh1). (13.2) Начальный объём, занимаемый газом, V1 = Sh1, а конечный V2 = Sh2. Поэтому можно выразить работу газа через изменение объёма ΔV = (V2 - V1): А' = p(V2 - V1) = pΔV > 0. (13.3) При расширении газ совершает положительную работу, так как направление силы и направление перемещения поршня совпадают. Если газ сжимается, то формула (13.3) для работы газа остаётся справедливой. Но теперь V2 < V1, и поэтому А < 0. Работа А, совершаемая внешними телами над газом, отличается от работы А' самого газа только знаком: А = -А' = -pΔV. (13.4)
При сжатии газа, когда ΔV = V2 - V1 < 0, работа внешней силы оказывается положительной. Так и должно быть: при сжатии газа направления силы и перемещения точки её приложения совпадают. Если давление не поддерживать постоянным, то при расширении газ теряет энергию и передаёт её окружающим телам: поднимающемуся поршню, воздуху и т. д. Газ при этом охлаждается. При сжатии газа, наоборот, внешние тела передают ему энергию и газ нагревается.
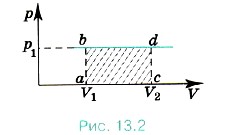
Геометрическое истолкование работы. Работе А' газа для случая постоянного давления можно дать простое геометрическое истолкование. При постоянном давлении график зависимости давления газа от занимаемого им объёма — прямая, параллельная оси абсцисс (рис. 13.2). Очевидно, что площадь прямоугольника abdc, ограниченная графиком рх = const, осью V и отрезками аb и cd, равными давлению газа, численно равна работе, определяемой формулой (13.3): А' = p1(V2 - V2) = |ab| • |ас|.
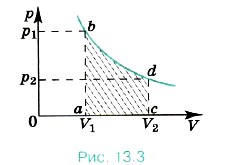
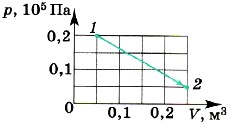
В общем случае давление газа не остаётся неизменным. Например, при изотермическом процессе оно убывает обратно пропорционально объёму (рис. 13.3). В этом случае для вычисления работы нужно разделить общее изменение объёма на малые части и вычислить элементарные (малые) работы, а потом все их сложить. Работа газа по-прежнему численно равна площади фигуры, ограниченной графиком зависимости р от V, осью V и отрезками аb и cd, длина которых численно равна давлениям p1 р2 в начальном и конечном состояниях газа.
Вопросы к параграфу 1. Почему газы при сжатии нагреваются? 2. Положительную или отрицательную работу совершают внешние силы при изотермическом процессе, изображённом на рисунке 13.3?
|
|
|



 Понаблюдайте за изменением температуры насоса при накачивании велосипедной камеры.
Понаблюдайте за изменением температуры насоса при накачивании велосипедной камеры.
 При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
При сжатии или расширении меняется и средняя потенциальная энергия взаимодействия молекул, так как при этом меняется среднее расстояние между молекулами.
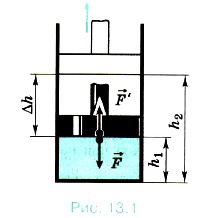
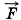 , действующей на газ со стороны внешнего тела (поршня), в зависимости от изменения объёма на примере газа в цилиндре под поршнем (рис. 13.1), при этом давление газа поддерживается постоянным. Сначала вычислим работу, которую совершает сила давления газа, действуя на поршень с силой
, действующей на газ со стороны внешнего тела (поршня), в зависимости от изменения объёма на примере газа в цилиндре под поршнем (рис. 13.1), при этом давление газа поддерживается постоянным. Сначала вычислим работу, которую совершает сила давления газа, действуя на поршень с силой  Объясните, почему процесс расширения газа должен происходить очень медленно.
Объясните, почему процесс расширения газа должен происходить очень медленно.