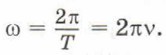|
|
|
|
|
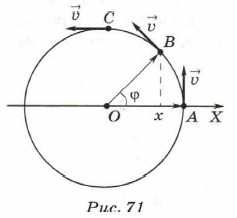
Глава 3. Электромагнитные колебания и волны § 19. Гармонические колебанияУравнение гармонических колебаний1. Выясним, как зависит координата колеблющегося тела от времени. Для этого проведём аналогию между колебательным и вращательным движениями. Предположим, что некоторая точка движется по окружности с постоянной по модулю линейной скоростью v. При этом проекция на ось ОХ точки, находящейся на окружности, совершает колебательное движение вдоль этой оси. Период обращения точки по окружности Т, радиус окружности — хm. Пусть в начальный момент времени точка находилась в положении А (рис. 71).
Её координата равна хm. В момент времени t точка будет находиться в положении В и её координата равна некоторому значению х. За время t радиус-вектор ОА повернётся на угол φ, поэтому проекция радиуса-вектора ОB на ось ОХ равна х = OBcos φ или х = xmcos φ. Из курса физики основной школы вы знаете, что физическую величину, равную отношению угла поворота радиуса-вектора к промежутку времени, за которое этот поворот произошёл, называют угловой скоростью. Обозначают угловую скорость буквой ω, её единица в СИ — радиан в секунду (рад/с). Следовательно, угол поворота точки φ = ωt и уравнение колебаний имеет вид
Оно выражает зависимость координаты колеблющегося тела от времени. Зависимость координаты колеблющегося тела от времени может выражаться и через синус. Вид тригонометрической функции зависит от начального состояния колебательной системы: если в начальный момент времени смещение относительно положения равновесия максимально, то в уравнении стоит косинус; если в начальный момент времени система находилась в состоянии равновесия, то в уравнение удобнее поставить синус.
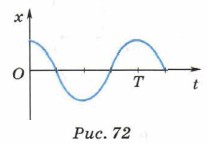
Графиком зависимости смещения при гармоническом колебании от времени является косинусоида (синусоида) (рис. 72).
Величину, состоящую в уравнении колебаний под знаком косинуса (или синуса), называют фазой колебаний φ.
Единица фазы в СИ — радиан (рад). Величину ω называют циклической частотой колебаний. Чтобы понять физический смысл этой величины, следует вспомнить, что значения косинуса (или синуса) повторяются при изменении аргумента на 2π. Например, в момент времени t = 0 координата тела, совершающего гармонические колебания, равна х = xmcos (ω • 0) = xmcos 0 = хm. Тело вернётся в точку с той же координатой, совершив одно полное колебание, т. е. через время, равное периоду Т: х = xmcos ωТ. Значения аргументов в моменты времени t = 0 и t = Т должны отличаться на 2π, т. е.: ωТ - 0 = 2π, или ωT = 2π. Откуда
Таким образом,
Единица циклической частоты в СИ — радиан в секунду (рад/с).
|
|
|