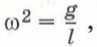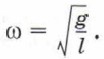|
|
|
|
|
Глава 3. Электромагнитные колебания и волны Гармонические колебанияСкорость и ускорение при гармонических колебаниях2. Вернёмся к аналогии между вращательным и колебательным движениями, чтобы записать уравнение скорости колеблющегося тела. Как видно из рисунка 71, проекция на ось ОХ вектора скорости движения точки в положении А равна нулю, а в положении С она максимальна, однако направлена в сторону, противоположную смещению. Следовательно, если координата колебаний проекции на ось ОХ точки, движущейся по окружности, изменяется по закону косинуса х = xmcos ωt, то её скорость изменяется по закону синуса с обратным знаком, υ = -υmsin ωt. Как вы знаете, ускорение колебательного движения прямо пропорционально смещению с обратным знаком, поэтому а ~ х или а ~ xmcos ωt, т. е. а = -аm cos ωt. Таким образом, скорость и ускорение колебательного движения, так же как и смещение, изменяются по гармоническому закону. Выясним, чему равны амплитудные значения скорости и ускорения. За время, равное периоду колебаний Т, точка, двигаясь по окружности, делает один оборот, а её проекция совершает одно полное колебание. За это время точка проходит путь S, равный длине окружности, т. е. S = 2πR или S = 2πхm. Соответственно линейная скорость движения точки по окружности υ равна максимальной скорости колебаний проекции этой точки на ось ОХ:
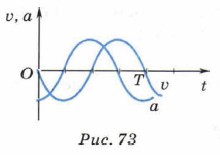
За это же время, равное периоду, радиус-вектор точки поворачивается на угол, равный 2л, и угловая скорость точки и соответственно циклическая частота колебаний равна Центростремительное ускорение, с которым точка движется по окружности, и соответственно амплитуда ускорения колебаний его проекции равна аm = ω2хm. Это равенство справедливо и для мгновенных значений смещения и ускорения: а = ω2x. Учитывая полученные выражения для амплитудных значений скорости и ускорения колебаний, перепишем уравнения зависимости скорости и ускорения колебаний от времени: υ = -ωxmsin ωt; а = -ω2xmcos ωt. На рисунке 73 приведены графики зависимости скорости и ускорения от времени при гармонических колебаниях.
Уточним физический смысл понятия фазы колебаний. Из полученных уравнений видно, что при заданной амплитуде гармонических колебаний, зная фазу колебаний, можно в любой момент времени определить значения смещения, скорости и ускорения колебаний. Таким образом,
Собственная частота колебательной системы3. Выведенная из состояния равновесия колебательная система совершает свободные колебания с определённой частотой. Эта частота определяется параметрами системы, поэтому её называют собственной частотой колебательной системы. Приравнивая выражения для ускорения
Следовательно, собственная частота пружинного маятника зависит от параметров колебательной системы — массы груза и жёсткости пружины. Аналогично можно записать формулу, выражающую зависимость частоты колебаний математического маятника от параметров этой колебательной системы. Напомним, что в данном случае колебательной системой является система «маятник — Земля». Поскольку
откуда
|
|
|



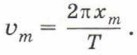
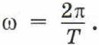 Подставив это равенство в формулу скорости, получим υm = ωхm.
Подставив это равенство в формулу скорости, получим υm = ωхm.
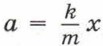 и а = ω2x, можно сделать вывод, что для пружинного маятника собственная частота колебаний определяется равенством
и а = ω2x, можно сделать вывод, что для пружинного маятника собственная частота колебаний определяется равенством
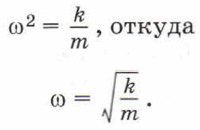
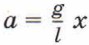 и а = ω2x, можно записать
и а = ω2x, можно записать