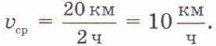|
|
|
|
|
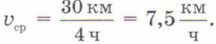
§ 11. Неравномерное движение Задачи, которые могут показаться одинаковымиРассмотрим две часто встречающиеся задачи на нахождение средней скорости. Задачи эти разные, но могут показаться одинаковыми — в этом и заключается их главная трудность. РЕШИМ ЗАДАЧИ Школьник в течение часа ехал на велосипеде со скоростью 15 км/ч, а потом ещё час шёл пешком со скоростью 5 км/ч. Найдём его среднюю скорость за всё время движения. Р е ш е н и е. За 2 ч школьник преодолел 20 км. Поэтому Обратите внимание: если на двух участках тело двигалось с различными скоростями одинаковое время, то средняя скорость тела равна среднему арифметическому скоростей на этих участках. Школьник сначала ехал на велосипеде со скоростью 15 км/ч, а потом шёл пешком со скоростью 5 км/ч. Найдём среднюю скорость за всё время движения, если 15 км школьник проехал и столько же прошёл. Р е ш е н и е. Первую половину пути (15 км) школьник проехал за 1ч, а вторую половину (тоже 15 км) прошёл за 3 ч. Значит, на весь путь школьник затратил 4 ч. Поэтому Обратите внимание: если на двух участках тело двигалось с различной скоростью и прошло при этом одинаковый путь, то средняя скорость тела не равна среднему арифметическому скоростей на этих участках. Почему же во второй задаче средняя скорость школьника меньше, чем в первой? Дело в том, что по условию первой задачи школьник ехал и шёл одинаковое время (по 1 ч), а из условия второй задачи следует, что он шёл в 3 раза дольше, чем ехал. А поскольку шёл он с меньшей скоростью, чем ехал, его средняя скорость во второй задаче оказалась меньшей.
|
|
|