|
|
|
|
|
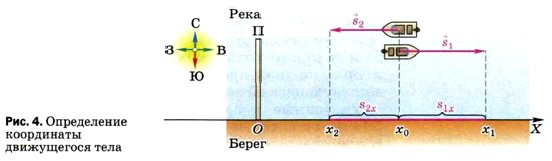
Глава 1. Законы взаимодействия и движения тел § 3. Определение координаты движущегося телаВ предыдущем параграфе говорилось о том, что положение тела, совершившего некоторое перемещение, можно найти графически, отложив вектор перемещения от начального положения этого тела. Но в большинстве случаев необходимо вычислить положение тела, т. е. определить его координаты. Известно, что вычисления производят не с векторами, а с соответствующими им скалярными величинами: с проекциями векторов на координатные оси и с модулями векторов или их проекций (т. е. с величинами, представляющими собой положительные или отрицательные числа, но не имеющими направления). Покажем, как определить координату движущегося тела, зная координату его начального положения и вектор перемещения. Для этого решим задачу. Два катера идут по реке в противоположных направлениях и встречаются в 100 км к востоку от пристани П (рис. 4). Продолжая движение, за некоторый промежуток времени t первый катер переместился от места встречи на 60 км к востоку, а второй — на 50 км к западу. Определите координаты каждого катера относительно пристани и расстояние между катерами через промежуток времени t после их встречи. Проведём координатную ось ОХ параллельно прямой, вдоль которой движутся катера, и направим её на восток. Начало этой оси (х = 0) — точку О — совместим с пристанью, приняв её за тело отсчёта (поскольку в задаче требуется определить положение катеров по отношению к пристани).
Спроецировав начала и концы векторов перемещения Значит, в данном случае s1x > 0, a s2x < 0. Из рисунка 4 видно, что координаты х1 и х2 можно найти следующим образом: х1 = x0 + s1x, (1)
Расстояние
По уравнениям (1) и (2) можно рассчитать искомые координаты х1 и х2. Но какие числа следует подставить в уравнения (1) и (2) вместо символов х0, s1x и s2x? Согласно условию задачи катера встретились на расстоянии 100 км от пристани, значит, длина отрезка Ох0 равна 100 км. Из рисунка 4 видно, что координата х0 находится на положительной полуоси ОХ, т. е. х0 > 0. Значит, х0 = 100 км. Поскольку ось ОХ параллельна векторам перемещений катеров, длины проекций s1x;c и s2x равны соответственно длинам векторов Указанные в задаче расстояния (60 км и 50 км), на которые сместились катера за время t, представляют собой модули векторов их перемещений. Значит, модуль проекции s1x равен 60 км, а модуль проекции s2x равен 50 км. Поскольку проекция s1x положительна, то можно записать: s1x = 60 км. Но проекция s2x отрицательна, поэтому s2x = -50 км. Теперь запишем условие задачи и решим её.
Вопросы1. С какими величинами производят вычисления — с векторными или скалярными?
Упражнение 31. Мотоциклист, переехав через мост, движется по прямолинейному участку дороги. У светофора, находящегося на расстоянии 10 км от моста, мотоциклист встречает велосипедиста. За 0,1ч с момента встречи мотоциклист перемещается на 6 км, а велосипедист — на 2 км от светофора (при этом оба они продолжают двигаться прямолинейно в противоположных направлениях). Определите координаты мотоциклиста и велосипедиста и расстояние между ними спустя 0,1ч после их встречи. У к а з а н и е: начертите ось X, направив её в сторону движения мотоциклиста и приняв за тело отсчёта мост. Обозначьте на этой оси координату светофора (хс), координаты велосипедиста (хв) и мотоциклиста (хм), которые они имели через 0,1ч после встречи. Над осью начертите и обозначьте векторы перемещений велосипедиста
2. Мальчик держит в руках мяч на высоте 1 м от поверхности земли. Затем он подбрасывает мяч вертикально вверх. За некоторый промежуток времени t мяч успевает подняться на 2,4 м от своего первоначального положения, достигнув при этом точки наибольшего подъёма, и опуститься от этой точки на 1,25 м (рис. 5). Пользуясь этим рисунком, определите: а) координату х0 начального положения мяча; б) проекцию stx вектора перемещения
|
|
|



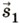 и
и 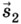 на ось ОХ, получим отрезки s1x и s2x, которые являются проекциями указанных векторов. Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси.
на ось ОХ, получим отрезки s1x и s2x, которые являются проекциями указанных векторов. Проекция вектора на ось считается положительной, если вектор сонаправлен с этой осью, и отрицательной, если вектор направлен противоположно оси.
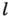 между двумя телами, как известно, равно модулю разности их координат:
между двумя телами, как известно, равно модулю разности их координат:

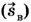 и мотоциклиста
и мотоциклиста 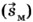 , а на оси — проекции этих векторов (sвх и sмx).
, а на оси — проекции этих векторов (sвх и sмx).
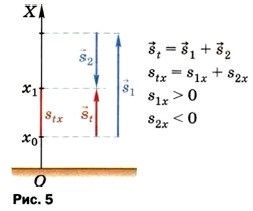
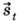 , совершённого мячом за время t; в) координату хt, которую имел мяч через промежуток времени t после броска.
, совершённого мячом за время t; в) координату хt, которую имел мяч через промежуток времени t после броска.