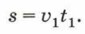|
|
|
|
|
Глава 1. Законы взаимодействия и движения тел § 4. Перемещение при прямолинейном равномерном движенииВо всех рассмотренных нами примерах и задачах по определению координат тела вектор перемещения был известен (т. е. были известны его модуль и направление). А как найти вектор перемещения, если он не задан? Проще всего получить формулу для определения вектора перемещения для тела, движущегося прямолинейно и равномерно (т. е. движущегося по прямолинейной траектории и проходящего за любые равные промежутки времени одинаковые пути). Согласно определению,
Из формулы (1) можно найти перемещение для прямолинейного равномерного движения:
При решении большинства задач на нахождение векторных величин (перемещения, скорости, силы и др.) необходимо знать, как эти величины направлены по отношению друг к другу. Об этом можно судить, в частности, по уравнениям, записанным в векторной форме. Например, формулы (1) и (2) свидетельствуют о том, что при прямолинейном равномерном движении векторы скорости и перемещения направлены в одну и ту же сторону. Но для расчёта перемещения применяют формулу, в которую входят проекции векторов на ось:
Напомним, что по знаку проекции можно судить о том, как направлен соответствующий ей вектор по отношению к выбранной оси. Но если при решении задачи на прямолинейное движение нас не интересует направление векторов перемещения и скорости, то можно воспользоваться формулой, в которую входят их модули:
Формула (4) вам давно знакома — вы часто использовали её при решении задач по физике и математике. Только под буквой s подразумевался пройденный телом путь. Почему же теперь мы говорим, что s — это модуль вектора перемещения? Дело в том, что при движении в одном направлении модуль вектора перемещения, совершённого телом за некоторый промежуток времени, равен пути, пройденному этим телом за тот же промежуток времени.
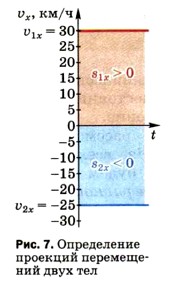
Справедливость этого утверждения наглядно иллюстрируется рисунком 3. Из этого рисунка видно, что в тех случаях, когда тело не меняет направления своего движения (т. е. при движении из точки О в точку А и из точки О в точку С), модуль вектора перемещения равен пройденному пути. Если же направление движения тела меняется (т. е. при переходе из точки О в точку В и обратно и при движении из точки О в точку D по криволинейной траектории), то пройденный путь окажется больше модуля вектора перемещения. На рисунке 6 представлен график зависимости модуля вектора скорости
Но произведение Таким образом, при прямолинейном равномерном движении тела модуль вектора его перемещения численно равен площади прямоугольника, заключённого между графиком скорости, осью Ot и перпендикулярами к этой оси, восставленными из точек, соответствующих моментам начала и конца наблюдения (в данном случае из точек О и t1). Часто эту площадь называют площадью под графиком скорости.
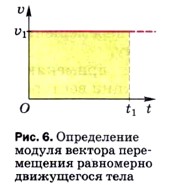
Поскольку при решении большинства задач придётся иметь дело не только с модулями, но и с проекциями векторов, рассмотрим график зависимости проекции вектора скорости от времени. Для этого обратимся ещё раз к задаче с двумя катерами, идущими прямолинейно и равномерно в противоположных направлениях (см. § 3, рис. 4). Допустим, что промежуток времени t, за который катера совершили указанные перемещения, равен 2 ч. За 2 ч первый катер переместился на 60 км, а второй — на 50 км. Значит, модуль вектора скорости первого катера равен 30 км/ч, а второго — 25 км/ч. Так как проекции векторов скорости и перемещения первого катера положительны, а второго — отрицательны, то Числовые значения проекций векторов скорости с соответствующими знаками, а также знаки проекций совершённых катерами перемещений, численно равных площадям под графиками, приведены на рисунке 7. Вопросы1. Что называется скоростью равномерного прямолинейного движения?
Упражнение 41. Может ли график зависимости модуля вектора скорости от времени располагаться под осью Ot (т. е. в области отрицательных значений оси скорости)? 2. Постройте графики зависимости проекций векторов скорости от времени для трёх автомобилей, движущихся прямолинейно и равномерно, если два из них едут в одном направлении, а третий — навстречу им. Скорость первого автомобиля равна 60 км/ч, второго — 80 км/ч, а третьего — 90 км/ч.
|
|
|







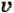 от времени t при равномерном движении тела. С такими графиками вы уже встречались при изучении физики в 7 классе (тогда их называли графиками зависимости скорости от времени).
Модуль вектора перемещения s, совершённого телом за промежуток времени t1, в данном случае определяется по формуле:
от времени t при равномерном движении тела. С такими графиками вы уже встречались при изучении физики в 7 классе (тогда их называли графиками зависимости скорости от времени).
Модуль вектора перемещения s, совершённого телом за промежуток времени t1, в данном случае определяется по формуле: