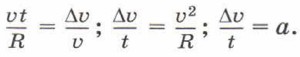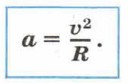|
|
|
|
|
Глава 1. Законы механики Движение тела по окружности с постоянной по модулю скоростьюБыстроту обращения тела характеризуют угловой скоростью.
Угловая скорость обозначается буквой ω.
За единицу угловой скорости в СИ принимают радиан в секунду (1 рад/с):
За время, равное периоду обращения Т, тело совершает полный оборот и угол поворота радиуса-вектора ω = 2π. Поэтому угловая скорость тела:
Линейная и угловая скорости связаны между собой. Запишем отношение линейной скорости к угловой:
Таким образом,
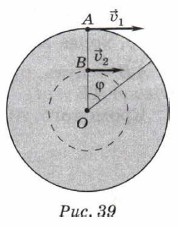
При одинаковой угловой скорости точек А и В, расположенных на равномерно вращающемся диске (рис. 39), линейная скорость точки А больше линейной скорости точки В: υ1 > υ2.
5. При движении тела по окружности с постоянной по модулю скоростью направление линейной скорости меняется. Поскольку скорость — величина векторная, то изменение направления скорости означает, что тело движется по окружности с ускорением. Выясним, как направлено и чему равно это ускорение. Напомним, что ускорение тела определяется по формуле:
где Δ Направление вектора Пусть тело, движущееся по окружности радиусом R, за малый промежуток времени t переместилось из точки А в точку В (рис. 40). Чтобы найти изменение скорости тела Δ
Рассмотрим треугольники АОВ и ACD. Оба они равнобедренные (АО = ОВ и АС = AD, поскольку υ0 = υ) и имеют равные углы: ∠АОВ = ∠CAD (как углы со взаимно перпендикулярными сторонами: АО ⊥
В том случае, когда точки А и В расположены близко друг к другу, хорда АВ мала и её можно заменить дугой Кроме того, АО = В, DC = Δυ, AD = υ. Следовательно,
Откуда ускорение тела
|
|
|



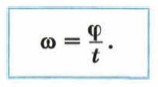
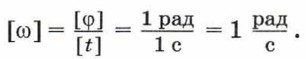
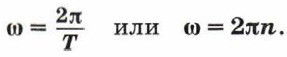
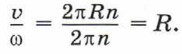
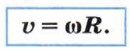
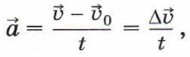
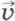 — вектор изменения скорости тела.
— вектор изменения скорости тела.
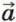 совпадает с направлением вектора Δ
совпадает с направлением вектора Δ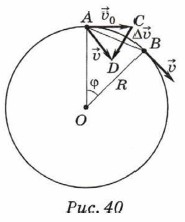
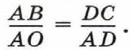
 . Длина дуги
. Длина дуги