|
|
|
|
|
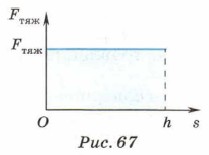
Глава 1. Законы механики Механическая работа и мощность4. Работу силы можно вычислить, используя график зависимости силы от перемещения. Предположим, под действием постоянной силы тяжести тело совершает перемещение. Графиком зависимости модуля силы тяжести Fтяж от модуля перемещения тела s является прямая, параллельная оси абсцисс (рис. 67). Найдём площадь выделенного прямоугольника. Она равна произведению двух его сторон: S = Fтяжh = = mgh. С другой стороны, этой же величине равна работа силы тяжести А = mgh.
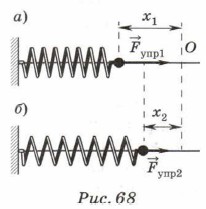
Таким образом, работа численно равна площади прямоугольника, ограниченного графиком, координатными осями и перпендикуляром, восставленным к оси абсцисс в точке h. Рассмотрим теперь случай, когда сила, действующая на тело, прямо пропорциональна перемещению. Такой силой, как известно, является сила упругости. Её модуль равен Fynp = kx, где х — удлинение тела. Предположим, пружину, левый конец которой закреплён, сжали (рис. 68, а). При этом её правый конец сместился на x1. В пружине возникла сила упругости Fynp1, направленная вправо.
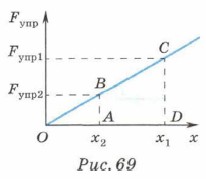
Если теперь предоставить пружину самой себе, то её свободный конец переместится вправо (рис. 68, б), удлинение пружины будет равно х2, а сила упругости Fynp2. Вычислим работу силы упругости при перемещении конца пружины из точки с координатой х1 в точку с координатой х2. Используем для этого график зависимости Fynp(х) (рис. 69).
Работа силы упругости численно равна площади трапеции ABCD. Площадь трапеции равна произведению полусуммы основании и высоты, т. е.
Таким образом, мы получили, что работа силы упругости равна:
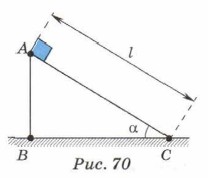
5*. Предположим, что тело массой т перемещается из точки А в точку В (рис. 70), двигаясь сначала без трения по наклонной плоскости из точки А в точку С, а затем без трения по горизонтальной плоскости из точки С в точку В. Работа силы тяжести на участке СВ равна нулю, поскольку сила тяжести перпендикулярна перемещению. При движении по наклонной плоскости работа силы тяжести равна: ААС = Fтяжlsin α.
Так как lsin α = h, то ААС = Fтяжh = mgh. Работа силы тяжести при движении тела по траектории АСВ равна ААСВ = ААС + АСВ = mgh + 0. Таким образом, ААСВ = mgh. Работа силы тяжести при перемещении тела из точки А в точку В по траектории АВ равна: ААВ = mgh. Полученный результат показывает, что работа силы тяжести не зависит от формы траектории. Она зависит только от начального и конечного положений тела. Предположим теперь, что тело движется по замкнутой траектории АВСА (см. рис. 70). При перемещении тела из точки А в точку В по траектории АСВ работа силы тяжести равна ААСВ = mgh. При перемещении тела из точки В в точку А сила тяжести совершает отрицательную работу, которая равна АВА = -mgh. Тогда работа силы тяжести на замкнутой траектории А = ААСВ + АВА = 0. Нулю равна и работа силы упругости на замкнутой траектории. Действительно, предположим, что недеформированную вначале пружину растянули и её длина увеличилась на х. Сила упругости при этом совершила работу
|
|
|



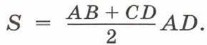 В трапеции ABCD основания АВ = Fynp2 = kx2, CD = Fynp1 = kx1, а высота AD = x1 — x2. Подставим в формулу площади трапеции эти величины:
В трапеции ABCD основания АВ = Fynp2 = kx2, CD = Fynp1 = kx1, а высота AD = x1 — x2. Подставим в формулу площади трапеции эти величины:
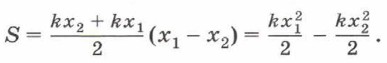
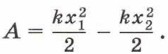
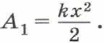 При возвращении в состояние равновесия сила упругости совершает работу
При возвращении в состояние равновесия сила упругости совершает работу 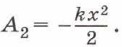 Суммарная работа силы упругости при растяжении пружины и её возвращении в недеформированное состояние равна нулю.
Суммарная работа силы упругости при растяжении пружины и её возвращении в недеформированное состояние равна нулю.