|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
Процентные ставки и методы их начисления 6.3.2. Области применения схемы простых процентов (продолжение)В практическом смысле эффект от выбора того или иного способа зависит от значительности суммы, фигурирующей в финансовой операции. Но и так ясно, что использование обыкновенных процентов с точным числом дней ссуды, как правило, дает больший результат, чем применение обыкновенных процентов с приближенным числом дней пользования кредитом. Пример Предоставлен кредит в размере 7 млн руб, 10 февраля с погашением 10 июня под 20% годовых (год невисокосный). Рассчитать разными способами сумму к погашению (FV). Решение Величина уплачиваемых за пользование кредитом процентов зависит от числа дней, которое берется в расчет. Точное число дней определяется но таблице с номерами дней года (см. Приложение 4): 161 — 41 = 120 дн. Приближенное число дней кредита рассчитывается следующим образом: 18 дней февраля (59 — 41)+ 90 дн. (по 30 дней каждого из трех месяцев: март, апрель, май) + 10 дней июня - 118 дн. Возможные варианты возврата долга определяются с помощью формулы (6.7): 1. В расчет принимаются точные проценты и точное число дней пользования кредитом.
2. В расчет принимаются обыкновенные проценты гг точное число дней пользования кредитом.
3. В расчет принимаются обыкновенные проценты и приближенное число дней пользования кредитом.
Учет векселя банком. Это еще одна весьма распространенная операция краткосрочного характера, для оценки которой используется схема простых процентов, с тем лишь отличием, что в расчете применяется дисконтная ставка. Одна из причин состоит в том, что векселя могут оформляться по-разному, однако чаще всего банку приходится иметь дело с суммой к погашению, т. е. с величиной FV. Схема действий в этом случае может быть следующей. Владелец векселя на сумму FV предъявляет его банку, который соглашается учесть его, т. е. купить, удерживая в свою пользу часть вексельной суммы, которая нередко также называется дисконтом. В этом случае банк предлагает владельцу сумму (PV), исчисляемую, исходя из объявленной банком ставки дисконтирования (d). Очевидно, что чем выше значение дисконтной ставки, тем большую сумму удерживает банк в свою пользу. Расчет выдаваемой банком суммы ведется с помощью одного из представлений формулы (6.8), являющейся следствием формулы (6.4):
Пример Векселедержатель предъявил для учета вексель на сумму 50 тыс. руб. со сроком погашения 28.09.2006 г. Вексель предъявлен 13.09.2006 г. Банк согласился учесть вексель по учетной ставке 30% годовых. Определить сумму, которую векселедержатель получит от банка. Величина этой суммы рассчитывается по формуле (6.8) и составит
Разность между FV (номинальной величиной векселя) и PV (дисконтированной величиной векселя) представляет собой комиссионные, удерживаемые банком в свою пользу за предоставленную услугу; в данном примере она составила 625 руб. Можно выполнить и более глубокий факторный анализ. Дело в том, что доход банка при учете векселя складывается из двух частей: процентов по векселю, причитающихся за время, оставшееся до момента погашения векселя, и собственно комиссионных за предоставленную услугу. Как уже упоминалось выше, теоретическая дисконтная ставка меньше процентной. Однако на практике, устанавливая дисконтную ставку, банк, как правило, повышает ее в зависимости от условий, на которых выдан вексель, риска, связанного с его погашением, комиссионных, которые банк считает целесообразным получить за оказанную услугу, и т. п. Поскольку величина процентов по векселю за период с момента учета до момента погашения предопределена, банк может варьировать лишь размером комиссионных путем изменения учетной ставки. Прежде чем рассмотреть пример, изложим логику факторного анализа дохода банка в этом случае. Введем следующие обозначения; PV — стоимость векселя в момент его оформления; Р1 — теоретическая стоимость векселя в момент учета; Р2 — предлагаемая банком сумма в обмен на вексель; FV — стоимость векселя к погашению;
|
|
|



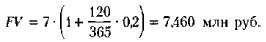
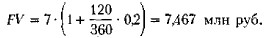
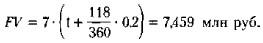

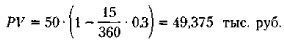
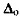 — общий доход банка от операции.
— общий доход банка от операции.