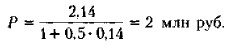|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
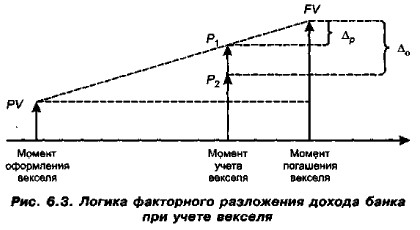
Процентные ставки и методы их начисления Области применения схемы простых процентовИз формул (6.7) и (6,8) видно, что функции PV = ƒ(t) и FV = g(t) являются линейными относительно t, т, е. процессы перехода PV → FV и FV → PV, а также cTpyicrypa факторного разложения при учете векселей могут быть представлены графически (рис, 6.3).
Скорость наращения стоимости векселя, т. е, наклон прямой {РРТ, FV}, зависит от уровня процентной ставки г, согласованной между векселедателем и векселедержателем. По мере приближения срока погашения векселя его теоретическая стоимость постоянно возрастает на сумму причитающихся за истекший период процентов; таким образом, в момент учета векселя она составит величину Р1, которую можно рассчитать по формуле (6.7). Таким образом, учитывая вексель в банке, его владелец теоретически мог бы рассчитывать на сумму P1, а факт ее получения означал бы, что с момента учета векселя кредитором векселедателя фактически становится банк. Вряд ли такое положение устраивает менеджеров банка, поскольку не очевидно, что заложенная в векселе доходность в размере ставки r будет привлекательна для банка. Именно поэтому предлагаемая банком сумма P2, которая рассчитывается по формуле (6.8), исходя из стоимости векселя к погашению и предлагаемой банком дисконтной ставки d, в принципе не связанной со ставкой r, в подавляющем большинстве случаев меньше теоретической стоимости векселя. Разность Пример Предприятие продало товар на условиях потребительского кредита с оформлением простою векселя: номинальная стоимость 150 тыс. руб., срок векселя — 60 дней, ставка процента за предоставленный кредит — 15% годовых. Через -15 дней с момента оформления векселя предприятие решило учесть вексель в банке; предложенная банком дисконтная ставка составляет: (1) 20%; (2) 25% годовых. Рассчитать суммы, получаемые предприятием и банком, если используются обыкновенные проценты с точным числом дней. Решение Будущая стоимость векселя FV к моменту его погашения, рассчитанная по формуле (6,7), составит
Срочная стоимость векселя Р1 в момент учета его банком, также рассчитанная по формуле (6.7), составит
Предлагаемая банком сумма Р2 рассчитывается по формуле (6.8):
Таким образом, банк получает от операции проценты по векселю за оставите- ся 15 дней в размере 937 руб. (153,75 - 152,813), величина которых не зависит от уровня дисконтной ставки, и комиссионные за оказанную услугу в размере в случае (1) — 344 руб. (152,813 - 152,469);
Дисконтирование, осуществляемое по формуле (6.8), называется батовским дисконтированием, в отличие от математического дисконтирования, являющегося процессом, обратным к наращению первоначального капитала. При математическом дисконтировании решается задача нахождения такой величины капитала Р, которая через n лет при наращении но схеме простых процентов но процентной ставке r будет равна Rn. Решая (6.5) относительно Р, получим
где n — необязательно целое число лет. Пример Через полгода после заключения финансового соглашения о получении кредита должник обязан заплатить 2,14 млн руб. Какова первоначалвная величина кредита, если он выдан под 14% годовых и начисляются обыкновенные проценты с приближенным числом дней? Решение Обозначая Rn = 2.14,
|
|
|



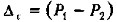 представляет собой сумму комиссионных, получаемых банком за услугу, оказываемую векселедержателю. С позиции последнего, эта сумма представляет собой затраты, т. е. плату за возможность более быстрого получения наличных. Помимо комиссионных банк получает проценты за период с момента учета до момента погашения векселя, сумма которых рассчитывается по формуле:
представляет собой сумму комиссионных, получаемых банком за услугу, оказываемую векселедержателю. С позиции последнего, эта сумма представляет собой затраты, т. е. плату за возможность более быстрого получения наличных. Помимо комиссионных банк получает проценты за период с момента учета до момента погашения векселя, сумма которых рассчитывается по формуле: 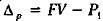 . Таким образом, общий доход банка от операции составит
. Таким образом, общий доход банка от операции составит 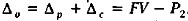 , Отметим, что реальные потери векселедержателя составляют величину
, Отметим, что реальные потери векселедержателя составляют величину 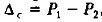 , а не сумму (FV — Р2), как это кажется на первый взгляд. Дело в том, что с момента учета векселя кредитором становится банк, поэтому ему и передаются проценты за оставшийся период.
, а не сумму (FV — Р2), как это кажется на первый взгляд. Дело в том, что с момента учета векселя кредитором становится банк, поэтому ему и передаются проценты за оставшийся период.
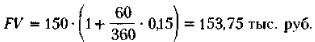
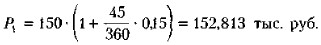
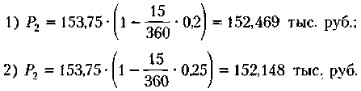

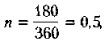 r = 0,14 и используя математическое дисконтирование, получим
r = 0,14 и используя математическое дисконтирование, получим