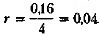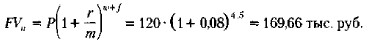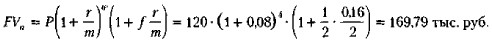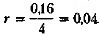Пример
Банк предоставил ссуду в размере 120 тыс, руб. на 27 мес. (т. е, 9 кварталов, или 2,25 года) под 16% годовых на условиях единовременного возврата основной суммы долга и начисленных процентов. Проанализировать, какую сумму предстоит вернуть банку при разных вариантах и схемах начисления процентов: (1) годовое; (2) полугодовое; (3) квартальное.
Решение
(1) Годовое начисление процентов
Продолжительность ссуды не является кратной продолжительности базисного периода, т. е. года. Поэтому возможно применение любой из схем, характеризуемых формулами (6.11) и (6.12) и значениями соответствующих параметров: n = 2,25 w = 2; ƒ = 0,25; r = 0,16
- При реализации схемы сложных процентов
FVn = P (1 + r)ω+ƒ = 120 • (1 + 0,1б)2,25 = 167,58 тыс. руб.
- При реализации смешанной схемы
FVn = Р (1 + r)ω (1 + ƒr) = 120 • (1 + 0,1 б)2 • (1 + 0,25 • 0,1б) = 167,93 тыс. руб.
(2) Полугодовое начисление процентов
Начисление процентов осуществляется по внутригодовым подпериодам, а продолжительность общего периода действия контракта не равна целому числу подпериодов. Следовательно, надо воспользоваться формулами (6.13) и (6.14), когда параметры формул имеют следующие значения: m = 2; ω = 4; ƒ = mn - ω = 2 • 2,25 - 4 = 0,5; r = 0,16.
- При реализации схемы сложных процентов
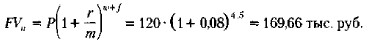
- При реализации смешанной схемы
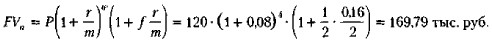
(3) Квартальное начисление процентов
В этом случае m = 2; ω = 9; ƒ = 0, т. е. продолжительность ссуды равна целому числу подпериодов. Поэтому формулы (6.13) и (6.14) дают один результат:
FVn = 120 • (1 + 0,04)9 = 170,8 тыс. руб.
Здесь фактически пользуемся обычной формулой наращения сложными процентами (6.6), в которой n = 9, a