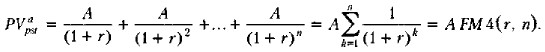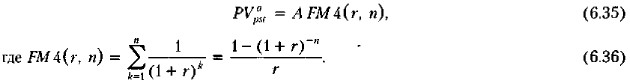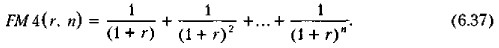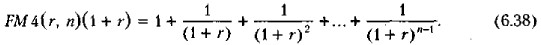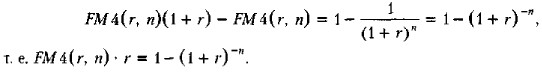|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
Оценка аннуитетов 6.7.1. Оценка срочного аннуитета (продолжение)Экономический смысл FM3(r, n), называемого мультиплицирующими множителем для аннуитета, заключается в следующем. Он показывает, чему будет равна суммарная величина срочного аннуитета в одну денежную единицу (например, один рубль) к концу срока его действия. Предполагается, что проводится лишь начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Множитель FM3(r, n) часто используется в финансовых вычислениях. Его значения зависят лишь от процентной ставки г и срока п действия аннуитета, причем с увеличением каждого из этих параметров величина FM3 (r, n) возрастает. Значения множителя для различных сочетаний r и n можно табулировать (см. Приложение 3). Из (6.30) следует, что FM3(r, n) показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления А. В связи с этим множитель FM3(r, n) называют также коэффициентом аккумуляции вкладов. Заметим, что формула (6.30) охватывает и пограничные случаи. Так, при одном денежном поступлении (n = 1) FM3(r, n) = 1 и Пример Вам предлагают сдать в аренду участок на 3 года, выбрав один из двух вариантов оплаты аренды: (1) 100 тыс. руб. в конце каждого года; (2) 350 тыс. руб. в конце периода. Какой вариант более предпочтителен, если банк предлагает 20% годовых по вкладам? Решение Первый вариант оплаты как раз и представляет собой аннуитет постнумерандо при n = 3 и A = 100 тыс. руб. Имеется возможность ежегодного получения арендного платежа и инвестирования полученных сумм на условиях 20% годовых (например, вложение в банк). К концу периода накопленная сумма может быть рассчитана в соответствии со схемой, аналогичной схеме, представленной на рис. 6.8.
Таким образом, расчет показывает, что вариант (1) более выгоден. Будущая стоимость аннуитета пренумерандо (т. е. денежного потока пренумерандо с равными элементами) представляет собой сумму наращенных элементов потока, исчисляемую в предположении, что: (а) все элементы одинаковы, (б) каждый элемент потока начинается в начале соответствующего базисного интервала и (в) наращение осуществляется по схеме сложных процентов с использованием заданной процентной ставки r. Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.10 в предположении, что CFk = А = const. Как было показано в разд. 6.6, значения будущей стоимости потоков пренумерандо и постнумерандо отличаются на множитель (1 + r), т. е. будущая стоимость денежного потока пренумерандо рассчитывается по формуле
Пример Ежегодно в начале года в банк делается очередной взнос в размере 10 тыс. руб. Банк платит 20% годовых. Какая сумма будет на счете по истечении 3 лет? Решение В данном случае мы имеем дело с аннуитетом пренумерандо, будущую стоимость которого предлагается оценить. В соответствии с формулой (6.34) найдем искомую сумму S: S = 10 • FM3(20%,3) • (1 + 0,2) = 10 • 3,640 • 1,2 = 43,68 тыс. руб. Дисконтированная стоимость аннуитета постнумерандо (Present Value of Ordinary Annuity) (т. e. денежного потока постнумерандо с равными элементами) представляет собой сумму приведенных к началу финансовой операции элементов потока, исчисляемую в предположении, что: (а) все элементы одинаковы, (б) каждый элемент потока начинается в конце соответствующего базисного интервала и (в) дисконтирование осуществляется по схеме сложных процентов с использованием заданной процентной ставки r. Для демонстрации логики расчета можно воспользоваться графиком на рис. 6.9 в предположении, что CFk = А = const, а горизонт планирования равен n.
Итак,
Вывод формулы (6.36) очевиден. Действительно,
Домножим обе части уравнения (6.37) на (1 + r), тогда получим:
Вычтя из уравнения (6.38) уравнение (6.37), получим
Отсюда и следует формула (6.36).
|
|
|



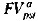 = А. Если r = 0, т.е.
не происходит наращения, из (6.30) получаем
= А. Если r = 0, т.е.
не происходит наращения, из (6.30) получаем