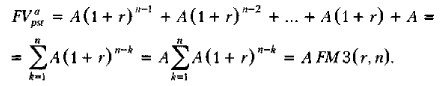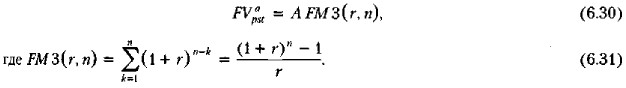|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
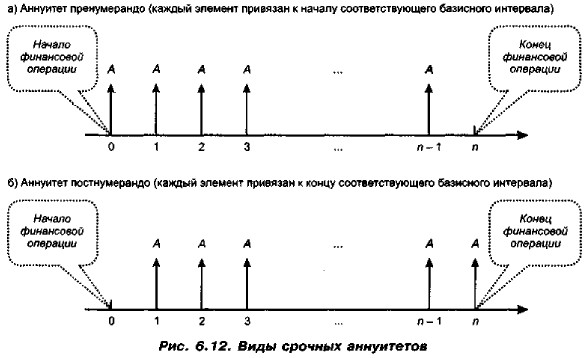
Оценка аннуитетов 6.7.1. Оценка срочного аннуитетаОценка аннуитетовОдним из ключевых понятий в финансовых и коммерческих расчетах является понятие аннуитета. Логика, заложенная в схему аннуитетных платежей, широко используется при оценке долговых и долевых ценных бумаг, в анализе инвестиционных проектов, а также в анализе аренды. Оценка срочного аннуитетаАннуитет (иногда в литературе используются термины «рента», «финансовая рента») представляет собой частный случай денежного потока. Известны два подхода к его определению. Согласно первому подходу аннуитет представляет собой однонаправленный денежный поток, элементы которого имеют место через равные временные интервалы. Второй подход накладывает дополнительное ограничение: элементы денежного потока одинаковы по величине, В дальнейшем изложении материала мы будем придерживаться именно второго подхода. Любой элемент денежного потока называется членом аннуитета (членом ренты), а величина постоянного временного интервала между двумя его последовательными элементами называется периодом аннуитета (периодом ренты). Если каждый элемент аннуитета имеет место в конце соответствующего периода, аннуитет называется аннуитетом постнумерандо (Ordinary Annuity); если в начале периода — аннуитетом пренумерандо (Annuity Due), Аннуитет, все элементы которого равны между собой, называется постоянным; если равенства нет, аннуитет носит название переменного. Пример аннуитета пренумерандо: накопление денег на банковском счете, когда вклады делаются, например, в начале каждого месяца. Пример аннуитета постнумерандо: регулярное получение процентов по ценной бумаге (по вкладу) по итогам очередного месяца. Если число равных временных интервалов ограничено, аннуитет называется срочным; в противном случае аннуитет носит название бессрочного. Для срочного аннуитета; CF1 = CF2 = ... = CFn = А. Графическое представление срочного аннуитета пост- и пренумерандо приведено на рис. 6.12. Вновь обращаем внимание читателя на то, что в обоих случаях финансовая операция, описываемая аннуитетом, начинается в точке 0 и заканчивается в точке п (грубо говоря, делая графические построения и проводя расчеты, всегда надо помнить о нехитром правиле; число стрелок и количество базисных интервалов должно совпадать). Примером срочного аннуитета постнумерандо могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении очередного периода. В качестве срочного аннуитета пренумерандо выступает, например, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления суммы для крупной покупки. Исторически вначале рассматривались ежегодные денежные поступления (базисный период принимался равным одному году), что и послужило основой для поименования потока аннуитетом («год» на латинском языке — anno). В дальнейшем в качестве периода стал выступать любой промежуток времени при сохранении прежнего названия.
Как и в случае с нетшшзированным денежным потоком, в отношении аннуитетов имеют место прямая и обратная задача. Специфика аннуитета (равенство денежных поступлений) позволяет вывести стандартизованные формулы, существенно упрощающие счетные процедуры. Логика рассуждений точно такова, как и в разд. 6.6. Будущая стоимость аннуитета постнумерандо (т. е. денежного потока постнумерандо с равными элементами) представляет собой сумму наращенных элементов потока, исчисляемую в предположении, что: (а) все элементы одинаковы, (б) каждый элемент потока начинается в конце соответствующего базисного интервала и (в) наращение осуществляется по схеме сложных процентов с использованием заданной процентной ставки r. Для демонстрации логики расчета можно воспользоваться графиком на рис, 6.8 в предположении, что CFk = А = const, а горизонт планирования равен n.
Итак,
Вывод формулы (6.31) очевиден. Действительно, FM3(r, n) = (1 + r)n-1 + (1 + r)n-2 + ... + (1 + r) + 1. (6.32) Домножив обе части уравнения (6.32) на (1 + r), получим FA/3(r,n) = (1 + r) = (1+ r)n + (1 + r)n-1 + ... +(1 + r)2 + (1 + r). (6.33) Вычтя из уравнения (6.33) уравнение (6.32), получим FM3(r,n)(1+ r) - FM3(r,n) = (1 + r)n - 1.
Отсюда и следует формула (6.31).
|
|
|