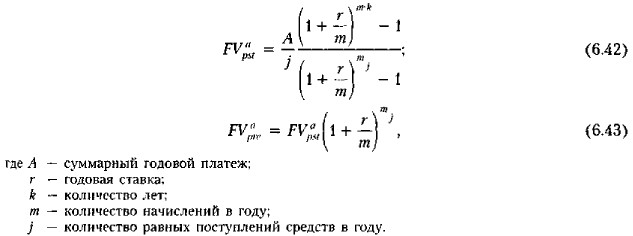|
|
|
|
Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В. |
|
|
Глава 6. Логикa и технике финансовых вычислений Логика оценки денежного потока в нетиповых ситуацияхВ теории финансовых вычислений разработаны унифицированные формулы, позволяющие упростить расчеты в случаях, когда имеет место несовпадение моментов поступления платежей (т. е. элементов денежного потока) и начисления процентов. Для потоков постнумерандо и пренумерандо в случае применения схемы сложных процентов эти формулы имеют соответственно вид
Предлагаем читателю самостоятельно сделать расчеты с помощью формул (6.42) и (6.43) для данных только что рассмотренного примера (возможные незначительные расхождения объясняются приблизительностью значений факторных множителей из финансовых таблиц). Несмотря на наличие специальных формул, мы посчитали целесообразным в подробностях рассмотреть логику и технику расчетов в примере. Причина в том, что нередко счетные формулы применяются механически, необдуманно. Подобное может приводить к заведомо неверным результатам. По нашему глубокому убеждению, финансовый аналитик должен уметь прогнозировать на качественном уровне исчисляемые результаты. Дело в том, что нередко для принятия решений финансового характера собственно цифра (число) не столь уж важна (например, с позиции точности). Важна тенденция, важно понимать логику операции, действия, алгоритма и заранее (если это возможно) делать суждение о том, что данная операция более выгодна, нежели альтернативная. Если хочется знать, насколько она выгодна, требуется более или менее точный расчет. Что касается сути проблемы соотношения частот поступления платежей и начисления процентов, проанализированной в примере, то несложно сделать очевидное обобщение; целесообразно выровнять продолжительность периода начисления процентов и периода поступления платежа. Для понимания логики процентных начислений можно, например, руководствоваться следующими правилами;
В заключение главы отметим, что приводимые в книге обозначения факторных множителей FM1(r, n), FM2(r, n), FM3(r, n), FM4(r, n) являются условными; в англоязычной и переводной литературе широко распространены следующие обозначения (в порядке соответствия): FVIF(r, n), PVIF(r, n), FVIFA(r, n), PVIFA(r, n), представляющие собой аббревиатуры соответствующих англоязычных наименований этих множителей: Future-Value Interest Factor, Future-Value Interest Factor for an Annuity, Present-Value Interest Factor, Present-Value Interest Factor for an Annuity. Заканчивая изложение материалов главы, еще раз сформулируем ключевые моменты, которые необходимо иметь в виду при проведении финансовых и коммерческих расчетов:
Наконец, хотелось бы особо подчеркнуть, что многие из рассмотренных алгоритмов финансовой математики не являются чем-то принципиально новым для отечественной науки и практики. Любопытному читателю можно порекомендовать обратиться к трудам профессора Н. С. Лунского, плодотворно работавшего в области теории и практики коммерческих и финансовых вычислений в первой четверти XX в. Лунского по праву можно считать одним из родоначальников финансового анализа в России (см. Библиографию).
|
|
|