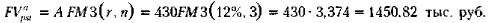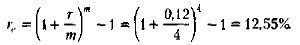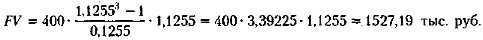Главная >> Финансовый менеджмент: теория и практика. Ковалев. В.В.

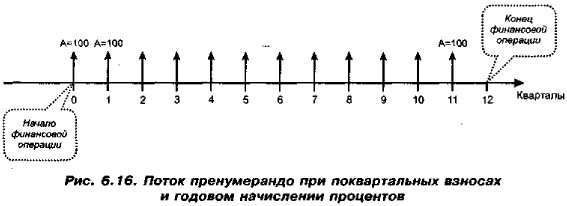
Глава 6. Логикa и технике финансовых вычислений

6.8. Логика оценки денежного потока в нетиповых ситуациях (продолжение)

Ситуация 2

Финансовая операция начинается в момент 0 и заканчивается в момент 12. Характеристики денежного потока таковы: поток представляет собой аннуитет пренумерандо с величиной аннуитетного платежа А = 100 тыс. руб.; число элементов потока равно 12; базисный интервал — квартал (см, рис. 6.16),

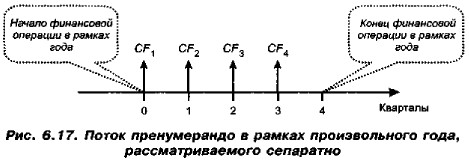
Здесь простейшие типовые формулы оценки будущей стоимости (как в ситуации 1) аннуитета уже не применимы, поскольку начисления процентов осуществляются лишь в моменты 4, 8 и 12. Для того чтобы понять логику наращения в этом случае, рассмотрим сепаратно один произвольный год, например первый. Денежный поток будет выглядеть следующим образом (рис. 6.17): (CF_k = A, k = 1,2,... 12)

Логика начисления процентов такова. Платеж CF₄ находится в банке один квартал, а потому при единовременном начислении процентов в конце года к нему должна быть применена квартальная ставка. Аналогично в отношении платежей CF₃, CF₂, CF₁ должны применяться соответственно ставка полугодовая, три четверти годовой ставки и годовая ставка. А потому к концу года на счете будет находиться сумма

S1 = 100 • (1 + 0,04) + 100 • (1 + 0,06)+ 100 • (1 + 0,08) + 100 • (1 + 0,12) =
= 100 • (1,04 + 1,06) + 1,08+ 1,12 = 100 • 4,3 = 430 тыс. руб.

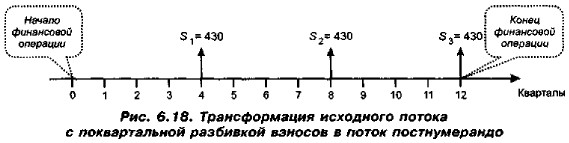
Подобное имеет место и в отношении других лет, рассматриваемых сепаратно, А потому исходный поток пренумерандо с величиной платежа 100 тыс. руб. и базисным интервалом квартал трансформируется в поток постнумерандо (рис. 6.18) с тремя аннуитетными платежами, величиной платежа 430 тыс. руб,, ставкой наращения 12% и базисным интервалом в 1 год.

Имеем аннуитет постнумерандо, будущая стоимость которого рассчитывается по формуле (6.30):

Сравнивая результаты расчетов в ситуациях 1 и 2, можно заметить, что вторая накопленная сумма оказалась меньше первой. Приведенный выше разбор счетного алгоритма объясняет причину этого. Разбиение годовой суммы на 4 части приводило к тому, что во второй ситуации относительно меньшая сумма в среднем была в распоряжении банка, поэтому естественно, что и меньшая сумма процентов была начислена.

Ситуация 3

Если рассматривать каждый год сепаратно, для расчета суммы, накопленной к концу года на счете, надо воспользоваться формулой (6.10). В разд. 6,3 было показано, что номинальной ставке с внутригодовыми начислениями соответствует эффективная ставка, исчисляемая по формуле (6.18) и предусматривающая однократное начисление

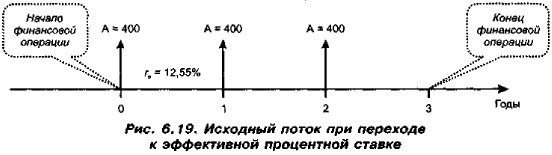
Таким образом, оцениваемый денежный поток представляет собой аннуитет пренумерандо с тремя аннуитетными платежами, величиной платежа А = 400 тыс, руб., базисным интервалом в 1 год н ставкой наращения r_e = 12,55% (рис. 6.19).

Для расчета итоговой суммы, накопленной на счете к концу 3-летнего периода, воспользуемся формулами (6.34) и (6.31):

Сравнивая сумму, исчисленную в данной ситуации, с предыдущими расчетными суммами, видим, что и здесь получили вполне оправданный результат. Ситуация 3 является самой выгодной с позиции накопления денежных средств, а причина выгодности в большей частоте начисления процентов.

<<< К началу      Окончание >>>