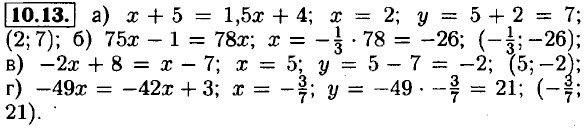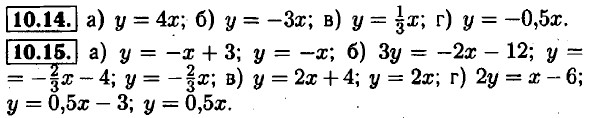Взаимное расположение графиков линейных функций

10.1. а) параллельны; б) пересекаются; в) совпадают; г) пересекаются

10.2. а) совпадают; б) пересекаются; в) параллельны; г) пересекаются

10.3. а) совпадают; б) пересекаются; в) параллельны; г) пересекаются

10.4. а) у = 8х - 3; б) у = 6х + 7; в) у = 12 - 7х; г) у = 4х + 11.

10.5. а) одинаковые; б) любое; в) противоположные; г) любое.

10.6. а) у = 4х - 3; б) у = 8х - 1; в) у = 5х - 4; г) у = 6х + 2.

10.7. а) любое; б) нет таких чисел; в) любое; г) нет таких чисел.

10.8. а) некорректно; б) 5; в) 6; г) некорректно.

10.9. а) некорректно; б) любое; в) любое; г) любое.

10.10. а) 2х + 3 = 3х + 2; x = 1, у = 2 • 1 + 3 = 5. (1; 5) ; б) прямые параллельны; в) 7х + 4 = -х + 4; х = 0, у = 7 • 0 + 4 = 4. (0; 4); г) прямые параллельны.

10.11. а) Прямые совпадают, следовательно, точек пересечения бесконечно много.

6) -3x + 4 = 2х - 1; 5x = 5; х = 1, у = 2 • 1 - 1 = 1. (1; 1).

в) Прямые совпадают, следовательно, точек пересечения бесконечно много.

г) -5х + 3 = x - 3; 6x = 6; х = 1, у = 1 - 3 = -2. (1; -2).

10.12. а) прямые параллельны, б) прямые совпадают; в) прямые параллельны; г) 79х = 75х; х = 0, у = 79 • 0 = 0. (0; 0).

10.16. а) у = 3x - 2; б) у = -2,5x + 6; в) у = -5x + 3; г) у = 1,5x + 3.

10.17. а) у = -2x - 2; б) у = 2x + 2; в) у = x + 1; г) у = -3x - 5.

10.18. k₁ = k₂; m₁ ≠ m₂.

10.19. k₁ = k₂; m₁ = m₂.

10.20. а) k₁ >0,k₂ > 0; k₁ ≠ k₂ б) k₁ ≤ 0; k₂ ≤ 0; k₁ ≠ k₂.

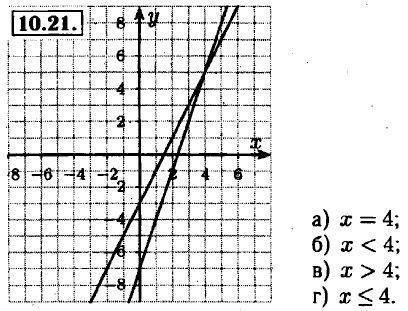
10.22. Из того что прямая у = ах + b проходит через начало координат следует, что 6 = 0. Значит, уравнение прямой имеет вид: у = ах.

Прямая у = ах. проходит через третий координатный угол (она там пересекается с прямой у = kх + m). Из этого следует, что a > 0.

Прямая у = kх + m проходит через третий координатный угол значит либо (k > 0) либо (k ≤ 0 и m ≤ 0). Но второй случай не подходит, потому что во втором случае прямая у = kх + m проходит через второй координатный угол.

Итак k > 0. Если m ≥ 0 то прямая проходит через второй координатный угол (если учитывать, что точка (0; 0) принадлежит второму координатному углу). Значит, m ≤ 0.

10.23. Прямая y = kх + m не проходит через третий координатный угол значит k ≤ 0 и m > 0 (считается что точка (0; 0) не принадлежит не одному из координатных углов). Рассмотрим прямую у = ах + b.

1. Случай а ≤ 0, тогда для того чтобы эта прямая проходила через первый координатный угол, необходимо чтобы b было больше 0.

2. Случай а > 0. Прямая всегда проходит через первый координатный угол. Но она также должна проходит

<<< К началу >>>