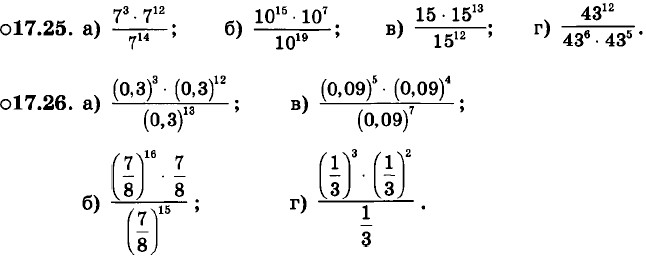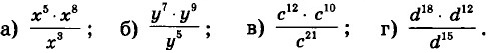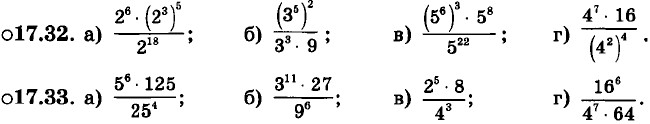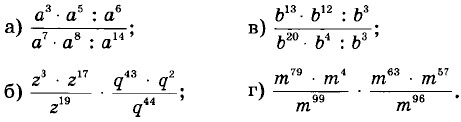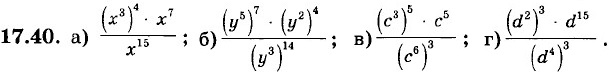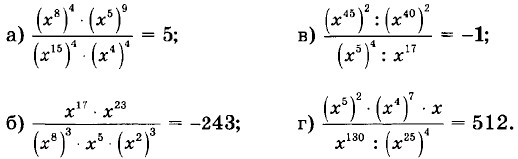Главная >> Алгебра 7 класс. Задачник с ГДЗ. Мордкович

Глава 4. Степень с натуральным показателем и её свойства

§ 17. Свойства степени с натуральными показателями (окончание)

Замените символ * степенью с основанием х так, чтобы выполнялось равенство:

17.21.

а) х5 : * = x3; б) x18 : * = х11;

в) x49 : * = x13; г) * : x5 = x99.

17.22.

а) * : x10 : * = x40; б) x44 • * • х : * = x51;

в) x45 : * : x15 • * = х; г) * : * : х = x73.

17.23. Каким должно быть натуральное число n, чтобы выпол нялось равенство:

а) 128n : 12856 = 12842; б) 2163 : 216n = 216;

в) 395n : 395 = 3959; г) 5484 : 548n = 5483.

17.24. Решите уравнение:

а) х : 2⁵ = 2³; б) 3^б : х = 3⁴; в) х : 5² = 5; г) 7⁷ : х = 7⁴.

17.27. Используя правила умножения и деления степеней, упростите выражение:

17.28. Запишите в виде степени с основанием х:

а) (х³)²; б) (x⁵)⁶; в) (х⁷)¹²; г) (x¹⁰)¹³.

17.29. Представьте 240 в виде степени с основанием:

а) 2⁸; б) 2¹⁰; в) 2²⁰; г) 2⁴.

17.30. Запишите в виде степени с показателем 3:

а) m¹⁸; б) n⁴⁸; в) а⁸⁴; г) b²¹.

Вычислите:

17.31. а) (7³)²; б) (3³)²; в) (4²)³; г) (2²)⁵.

17.34. Замените символ * таким выражением, чтобы выполнялось равенство:

а) (*)⁵ = а³⁰; б) (2^*)³ = z¹²; в) (*)⁷ = b¹⁴; г) (р¹²)^* = р²⁴.

17.35. Упростите выражение:

а) (а³)⁶ • а⁴; б) b⁵ • (b³)⁴; в) с⁶ • (с²)³; г) (d⁸)⁴ • d²³.

17.36. Используя правила умножения и деления степеней, упростите выражение:

17.37. Известно, что х² = у. Чему равно:

а) x⁶; б) х¹²; в) x²⁰; г) x⁴⁰?

Упростите выражение:

17.38.

а) (x5)4 • (x6)7; б) (у8)2 • (у12)3.

в) (z13)3 • (z5)9; г) (t25)2 • (t10)4.

17.39. а) (z⁵)⁶ : z⁷; б) (р³)⁴ : р¹⁰; в) (u¹⁴)3 : u²⁰; г) (q⁸)⁹ : q⁷⁰.

17.41. Возведите в степень:

а) (x³)ⁿ; б) (-а⁴)²ⁿ; в) (уⁿ)⁵; г) (-b³)⁶ⁿ.

17.42. Решите уравнение:

<<< К началу      Решенния >>>