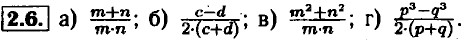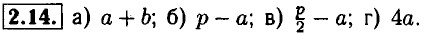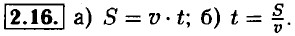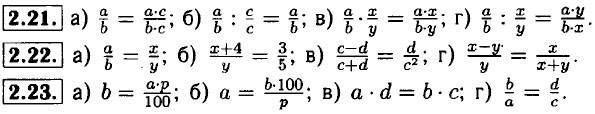Что такое математический язык

12.1. а) а + b; б) с - d; в) х • у; г) t : υ.

12.2. a) (z + x) : 2; б) (р - q) : 2; в) х²; г) у³.

2.3. а) х + а • b; б) у - а : 6; в) а • (b + с); г) z : (х - у).

2.4. а) (m + n) : 3; б) (р - q) • 2; в) (х + у) • 2 • z; г) р : (а + b) : 2.

2.5. а) (а + b)²; б) (х - у)³; в) t² - ω2; г) с³ + d³.

2.7. а) Сумма чисел х и 2. б) Разность чисел c и d. в) Произведение чисел 8 и z. г) Частное от деления числа р на q.

2.8. а) Сумма квадратов чисел а и b. б) Разность квадратов чисел х и у, в) Сумма кубов чисел z и t. г) Разность кубов чисел m и n.

2.9. а) Квадрат суммы чисел s и р. б) Квадрат разности чисел u и υ. в) Куб суммы чисел р и q. г) Куб разности чисел ƒ и q.

2.10. а) Отношение суммы чисел х и у к числу 2. б) Отношение разности чисел а и b к числу 2. в) Отношение произведения чисел х и у к их удвоенной разности, г) Отношение суммы чисел х и у к их произведению.

2.11. а) а + b = b + а; б) ab = bа; в) а + (b + с) = (а + b) + с; г) а + (b - с) = (а + 6) - с.

2.12. а) Чтобы к числу прибавить сумму двух чисел, можно сначала прибавить к нему первое слагаемое, а затем к полученной сумме второе слагаемое, б) Чтобы из числа вычесть сумму двух других чисел, можно сначала вычесть первое слагаемое, а затем из полученной разности вычесть другое слагаемое, в) При сложение любого числа а с нулем, получается тоже самое число а. г) При умножение любого числа а на единицу, получается тоже самое число а.

2.13. а) При умножении любого числа а на ноль получается ноль, б) Частное от деления нуля на любое число а не равное нулю, получается ноль, в) При делении любого числа а на единицу, получается тоже самое число а. г) При умножении любого числа а не равного нулю на частное от деления единицы на это же самое число а, получается единица.

2.15. a) S : а; б) а².

2.17. а) V = а³; б) S = 6а²; в) V = а • b • с; г) S = 2 • (а • Ь + b • с + а • с).

2.18. а) Произведение числа 3 и квадрата суммы чисел х и у. б) Произведение числа 2 и квадрата суммы чисел а и b. в) Произведение числа 2 и квадрата разности чисел р и q. г) Произведение числа 3 и квадрата разности чисел z и r.

2.19. а) Отношение квадрата разности чисел m и n к числу 2. б) Отношение квадрата суммы чисел t и ω к числу 2. в) Отношение куба суммы чисел а и b к числу 3. г) Отношение квадрата разности чисел р и q к числу 4.

2.20. а) (а + b) • с = а • c + b • c; б) х • (у - z) = х • у - х • z; в) а - (b + с) = (а - b) - с; г) а - (b - с) = (а - b) + с.

<<< К началу