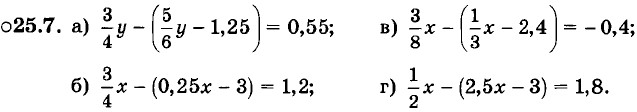§ 25. Сложение и вычитание многочленов

25.1. Найдите р(а) = p₁(a) + р₂(а), если:

а) p₁(a) = 2a + 5; р₂(а) = 3а - 7;
б) p₁(a) = 7 - 2а; р₂(а) = -1 - 5а;
в) P₁(a) = 3а - 4; р₂(а) = 11 - 3а;
г) Р₁(а) = -4 - 3а; р₂(а) = 7 - 8а.

25.2. Найдите р(х) = р₁(х) + р2(х), если:

а) р₁(х) = 2х³ + 5; р₂(х) = 3х³ + 7;
б) р₁(х) = 4x⁵ + 2х + 1; р₂(x) = х⁵ + х - 2;
в) p₁(х) = 6x² - 4; р₂(х) = 5x² - 10;
г) р₁(х) = х¹¹ + х⁶ - 3; р₂(х) = 2х¹¹ + 3х⁶ + 1.

25.3. Найдите р(а; b) = р₁(а; b) + р₂(а; b), если:

а) p₁(a; b) = а + 3b;
р₂(а; b) = 3а - 3b;
б) p₁(a; b) = 8а³ + 3а²b - 5аb² + b³;
р₂(а; b) = 18а³ - 3а²b - 5аb² + 2b³;
в) р₁(а; b) = а² - 5аb - 3b²;
р₂(а; b) = а² + b²;
г) р₁(а; b) = 10а⁴ - 7а³b - а²b² + 6;
р₂(а; b) = 17а⁴ - 10а³b + а²b² + 3.

25.4. Найдите р(у) = р₁(у) - р₂(у), если:

а) р₁(у) = 2у³ + 8у - 11; р₂(у) = 3у³ - 6у + 3;
б) р₁(у) = 4у⁴ + 4у² - 13; р₂(у) = 4у⁴ - 4у² + 13;
в) р₁(у) = у³ - у + 7; р₂(у) = у³ + by + 11;
г) р₁(у) = 15 - 7у²; р₂(у) = у³- у² - 15.

25.5. Найдите р(с; d) = р₁с; d) - р₂(с; d), если:

а) р₁(с; d) = 3с² + d; р₂(с; d) = 2с² - 3d;
б) р₁с; d) = 5с⁴ + 3c²d; р₂(с; d) = 2с² + 3c²d + d²;
в) р₁(с; d) = 12c²d - 3cd² + 4; р₂(с, d) = 6с²d - 5cd² + 2с;
г) р₁(с; d) = с² + 2cd + d²; р₂(с; d) = 5с² - 6cd - 7d².

Решите уравнение:

25.6. а) (5x - 3) + (7x - 4) = 8 - (15 - 11x);
б) (4х + 3) - (10x + 11) = 7 + (13 - 4x);
в) (7 - 10x) - (8 - 8x) + (10х + 6) = -8;
г) (2x + 3) + (3x + 4) + (5x + 5) = 12 - 7х.

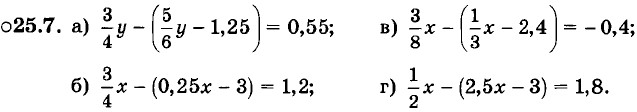
Окончание >>>