Глава 6. Многочлены. Арифметические операции над многочленами
§ 28. Формулы сокращённого умножения (окончание)
2 ;
2 + (m + 3n)(m - 3n).
2 + 25);
2 + 4);
2 );
г) (с2 - 1)(с2 + 1)(с4 + 1).
(2а - b)(2а + b) + (b - с)(5 + с) + (с - 2а)(с + 2а) = 0.
Упростите выражение и найдите его значение:
2 - (а - 2)(а + 2) при а = -3,5;
2 - (х + 3)(х - 3) при х = -0,1;
2 - (m - 9)(m + 9) при m = -0,5;
2 - (с + 4)(с - 4) при
2 - (3а - 8)2 + 132а при а = -6;
2 + (4р + 6)2 + 100р при р = -2;
2 + (12b - 4)2 - 4b при b = -1;
2 - (12 - 4m)2 + 4m при
а) 8x(1 + 2х) - (4х + 3)(4х - 3) = 2х;
Решите уравнение:
2 - х(х + 8) = 2;
2 = 1;
2 = 2;
2 = 1.
2 - 1 - (3х - 2)2 = 0;
2 = 25(1 + х2 );
2 - 2х(4 + 2х) = 11;
2 - х2 ;
2 - 4(х - 1)(х + 1) = 49;
2 - 4х2 = (2 - х)(2 + х);
2 - (3х - 2)(2 + 3х) = 17.
2 + х + 1) = 0;
2 - 2х + 4) = 7;
2 + 2х + 4) = 0;
2 - х + 1) = -7.
2 .
2 .
Преобразуйте выражение в многочлен стандартного вида:
28.50.
а) (10х2 - 3ху3 )2 ;
3 + 5p2 q)2 ;
в) (0,6b3 - 5b2 с4 )2 ;
7 + 0,5z3 t)2 .
28.52. а) (хn - 23 )(хn + 23 );
2n + bn )(а2n - bn );
n - d3n )(cn + d3n );
n + 1 - bn - 1 )(an + 1 + bn - 1 ).
28.53. а) (3х2 - 2)(9х4 + 6х2 + 4);
2 + 3)(25х4 - 15х2 + 9);
2 + 3)(64b4 - 24b2 + 9);
2 - 1)(49а4 + 7а2 + 1).
28.54. а) (х - 2)2 (х + 2)2 ;
2 (у + 4);
2 (m + 6)2 ;
2 (7 + n).
28.55. а) (х - у)(х + у)(х2 + у2 );
2 + b2 );
3 + q)(p3 - q)(p6 + q2 );
4 + r4 )(s - r)(s + r)(s2 + r2 ).
28.56. a) (3х2 + 4)2 + (3х2 - 4)2 - 2(3x2 + 4)(3x2 - 4);
2 + pc + c2 );
3 + 5)2 + (4a3 - 1)2 + 2(4a3 + 5)(4a3 - 1);
2 - 2(m + 1 )(m2 - m + 1).
28.57. a) (a - b)(a + b)(a2 + b2 )(a4 + b4 )(a8 + b8 );
32 - (x - 1)(x + 1)(x2 + 1)(x4 + 1)(x8 + 1)(x16 + 1).
Замените символы * одночленами так, чтобы выполнялось равенство:
28.58. а) (6а5 + *)2 = * + * + 25х2 ;
5 + *)2 = * + * + 36m4 n6 ;
7 )2 = 25х4 у2 - * + *;
3 - *)2 = * - * + 49а8 b6 .
28.59. а) (* + 4d4 )2 = * + 24c2 d5 + *;
4 )2 = 81а6b2 - * + *;
2 q2 + *)2 = * + * + 0,01q8 ;
4 t3 - *)2 = * - * + 0,16t4 .
28.60. а) (* + *)2 = * + 70b3 с + 49с2 ;
2 = 81х2 - * + 100х4 у6 ;
2 = * + 70х3 у2 + *;
2 = * - 48c5 d3 + *.
28.63. Найдите значение выражения:
а) (2 - 1)(2 + 1)(22 + 1)(24 + 1)(28 + 1) - 216 ;
2 + 1)(24 + 1)(28 + 1)(216 + 1) - 232 .
(32 + 22 )(34 + 24 )(38 + 28 )(318 + 216 ) = 0,2(332 - 232 ).
<<< К началу Решенния >>>



 28.38. а) (а - с)(а + с) - (а - 2с)2;
28.38. а) (а - с)(а + с) - (а - 2с)2;
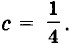
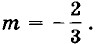
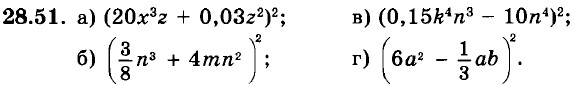
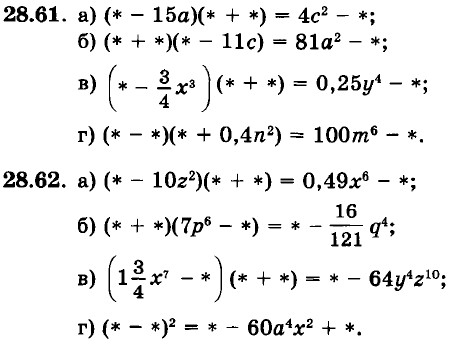
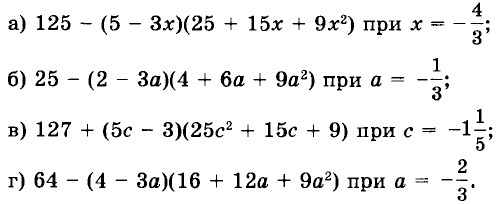
 28.64. Найдите значение числового выражения:
28.64. Найдите значение числового выражения: