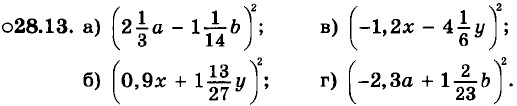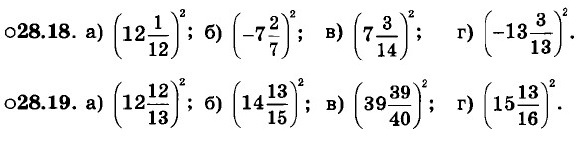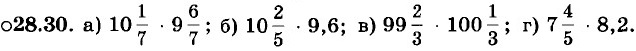|
Глава 6. Многочлены. Арифметические операции над многочленами



§ 28. Формулы сокращённого умножения
Преобразуйте квадрат двучлена в многочлен стандартного вида:
28.1. а) (а + х)2; б) (b - у)2; в) (с + d)2; г) (m - n)2.
28.2. а) (х + 1)2; б) (у - 2)2; в) (а - 5)2; г) (с + 8)2.
28.3. а) (7 - a)2; б) (9 + b)2; в) (4 + n)2; г) (12 - р)2.
28.4. а) (-x + 1)2; б) (-z - 3)2; в) (-n + 8)2; г) (-m - 10)2.
28.5. а) (2а + 1)2; б) (3с - 2)2; в) (6x - 3)2; г) (7у + 6)2.
28.6.
|
а) (8x + 3у)2;
б) (6m - 4n)2;
|
в) (9р - 2q)2;
г) (10z + 3t)2.
|
28.7.
|
а) (-3а + 5x)2;
б) (-6у - 2z)2;
|
в) (-3m + 4n)2;
г) (-12z - 3t)2.
|
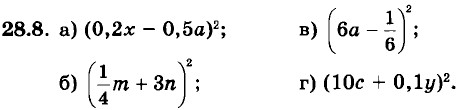
28.9.
|
а) (x2 + 1)2;
б) (у2 - 6)2;
|
в) (q2 + 8)2;
г) (р2 - 10)2.
|
28.10.
|
а) (а2 + 3x2;
б) (b2 - 5у)2;
|
в) (r2 + 4s)2;
г) (m2 - 6n)2.
|
28.11.
|
а) (с2 + d2)2;
б) (m2 - n3)2;
|
в) (z2 + t3)2;
г) (р2 - q2)2.
|
 28.12. 28.12.
|
а) (а3 + 3b)2;
б) (4x2 - 3с)2;
|
в) (5m2 + 3n2)2;
г) (6р2 - 8g3)2.
|
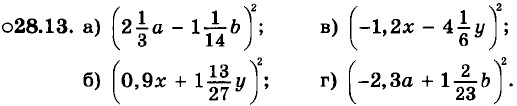
Используя формулы для (а ± b)2, вычислите:
28.14. а) 792; б) 392; в) 592; г) 692.
28.15. а) 212; б) 312; в) 612; г) 912.
28.16. а) 422; б) 622; в) 822; г) 322.
28.17. а) 982; б) 282; в) 882; г) 582.
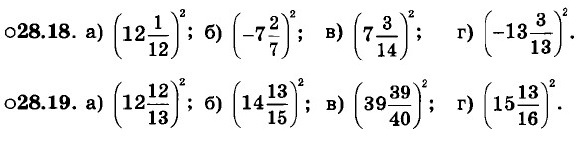
Выполните действия, используя соответствующую формулу сокращённого умножения:
28.20.
|
а) (а - b)(а + b);
б) (с - d)(c + d);
|
в) (m - n)(m + n);
г) (р - q)(p + q).
|
28.21.
|
а) (х - 1)(х + 1);
б) (9 - а)(9 + а);
|
в) (с - 2)(с + 2);
г) (12 - t)(12 + t).
|
28.22.
|
а) (3b - 1)(3b + 1);
б) (6x - 2)(6х + 2);
|
в) (10m - 4)(10m + 4);
г) (8а - 1)(8а + 1).
|
28.23.
|
а) (4а - b)(b + 4а);
б) (х + 7)(7 - х);
|
в) (4b + 1)(1 - 4b);
г) (5m + 2)(2 - 5m).
|
28.24.
|
а) (3х - 5у)(3х + 5у);
б) (7а - 8b)(7а + 8b);
|
в) (13с - 11d)(13c + 11d);
г) (8m - 9n)(8m + 9n).
|
 28.25. а) (5х - 2у2)(5х + 2у2); 28.25. а) (5х - 2у2)(5х + 2у2);
б) (2с - 3а2)(3а2 + 2с);
в) (10р3 - 7q)(10p3 + 7q);
г) (8d + 6с3)(6с3 - 8d).
 28.26. а) (4х2 - 2у2)(4х2 + 2у2); 28.26. а) (4х2 - 2у2)(4х2 + 2у2);
б) (10а3 + 5b2)(10а3 - 5b2);
в) (3n4 - m4)(3n4 + m4);
г) (10m8 + 8n8)(10m8 - 8n8).
Используя формулу (а + b)(а - b) = а2 - b2, вычислите:
28.27. а) 69 • 71; б) 31 • 29; в) 89 • 91; г) 99 • 101.
28.28. а) 58 • 62; б) 82 • 78; в) 42 • 38; г) 18 • 22.
 28.29. а) 0,49 • 0,51; б) 0,78 • 0,82; в) 0,67 • 0,73; г) 1,21 • 1,19. 28.29. а) 0,49 • 0,51; б) 0,78 • 0,82; в) 0,67 • 0,73; г) 1,21 • 1,19.
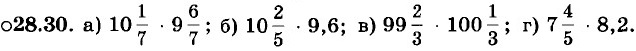
Выполните действия, используя соответствующую формулу сокращённого умножения:
28.31. а) (х - 1)(х2 + х + 1);
б) (х + 3)(х2 - 3х + 9);
в) (х - 2)(х2 + 2х + 4);
г) (х + 4)(х2 - 4х + 16).
28.32. а) (5m + 3n)(25m2 - 15mn + 9n2);
б) (2а - 3х)(4а2 + 6ах + 9х2);
в) (3х + 4у)(9х2 - 12ху + 16у2);
г) (4х - 5у)(16х2 + 20ху + 25у2).
Преобразуйте выражение в многочлен стандартного вида:
28.33.
|
а) 3(х - у)2;
б) -с(3а + с)2;
|
в) -6(5m - n)2;
г) d(1 + 25)2.
|
 28.34. 28.34.
|
а) а2 + (3а - b)2;
б) 9р2 - (q - 3р)2;
|
в) (5с + 7d)2 - 70cd;
г) (8m - n)2 - 64m2.
|
 28.35. 28.35.
|
а) (а - 4)2 + а(а + 8);
б) (х - 7)х + (х + 3)2;
|
в) (у - 5)2 - (у - 2);
г) b(b + 4) - (b + 2)2.
|
 28.36. а) (3а - 6)(3а + b) + b2; 28.36. а) (3а - 6)(3а + b) + b2;
б) 9х2 - (у + 4х)(у - 4х);
в) (5с - 6d)(5c + 6d) - 25с2;
г) (7m - 10n)(7m + 10n) - 100n2.
 28.37. а) 2(а - 2)(а + 2); 28.37. а) 2(а - 2)(а + 2);
в) 5с(с + 3)(с - 3);
б)x(x + 4)(x - 4);
г) 7d2(d - 1)(d + 1).
Окончание >>>
| 


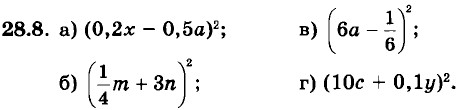
 28.12.
28.12.