|
Глава 6. Многочлены. Арифметические операции над многочленами



§ 29. Деление многочлена на одночлен
Выполните деление многочлена на одночлен:
29.1. а) (12а + 8) : 4;
б) (54d + 36) : (-18);
в) (44y + 22) : 11;
г) (-15 - 5у) : (-5).
29.2. а) (а - аb) : а;
б) (x - ху) : (-x);
в) (-m - mn) : m;
г) (-с + cd) : (-с).
29.3. а) (а2 + 3аb) : а;
б) (m3 - m2n) : m2;
в) (с2 - 2cd) : с;
г) (р4 - p3q) : р3.
 29.4. a) (4аb2 + 3аb) : (ab); 29.4. a) (4аb2 + 3аb) : (ab);
б) (1,2cd3 - 0,7cd) : (cd);
в) (-3,5m2n - 0,2mn) : (mn);
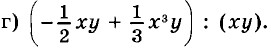
 29.5. a) (4x + 12у - 16) : (-4); 29.5. a) (4x + 12у - 16) : (-4);
б) (3x2y - 4ху2) : (5xy);
в) (2аb + 6а2b2 - 4b2) : (-2b);
г) (-а5b3 + 3а6b2) : (4а4b2).
 29.6. Найдите значение алгебраического выражения: 29.6. Найдите значение алгебраического выражения:
а) (18а4 - 27а3) : (9а2) - 10а3 : (5а) при а = -8;
б) (36x2y - 4ху2) : (4ху) + у при 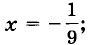 у = 0,2745. у = 0,2745.
 29.7. Придумайте три одночлена, на которые делится данный многочлен: 29.7. Придумайте три одночлена, на которые делится данный многочлен:
а) 5х2 - 6х4 + 48x6 - 12x3;
б) 14x6 - 28x + 7x5 + 84x4 - 56x8;
в) 15а2b3 + 25а4b2 - 30а6b3 - 75а4b7;
г) 45m6n2 + 30m3n5 + 60m4n3 - 90m4n5.
 29.8. Установите, корректно ли задание: разделить многочлен 2x3y2 + 3х2у - 5x4y4 на одночлен А, если: 29.8. Установите, корректно ли задание: разделить многочлен 2x3y2 + 3х2у - 5x4y4 на одночлен А, если:
29.9. Выполните почленное деление числителя дроби на знаменатель:
29.10. Установите, корректно ли предложенное задание, и если да, то выполните его:
а) (7а2 + 10а3b) : а4;
б) (4x2 - 3x) : (-x2);
в) (27а3 - 81b3) : (9а3b3);
г) (42x3y - 63xy3 + 14ху) : (7ху).
Окончание >>>
| 


 29.4. a) (4аb2 + 3аb) : (ab);
29.4. a) (4аb2 + 3аb) : (ab);
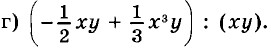
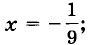 у = 0,2745.
у = 0,2745.