|
|
|
|
|
§ 4. Статистические характеристики Медиана как статистическая характеристикаРассмотрим ещё одну статистическую характеристику. Начнём с примера. В таблице показан расход электроэнергии в январе жильцами девяти квартир:
Составим изданных, приведённых в таблице, упорядоченный ряд:
В полученном упорядоченном ряду девять чисел. Нетрудно заметить, что в середине ряда расположено число 78: слева от него записано четыре числа и справа четыре числа. Говорят, что число 78 является срединным числом, или, иначе, медианой, рассматриваемого упорядоченного ряда чисел (от латинского слова mediana, которое означает «среднее»). Это число считают также медианой исходного ряда данных. Приведём теперь другой пример. Пусть при сборе данных о расходе электроэнергии к указанным девяти квартирам добавили ещё десятую. Получили такую таблицу:
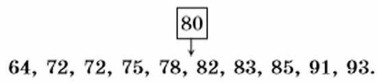
Так же как в первом случае, представим полученные данные в виде упорядоченного ряда чисел:
В этом числовом ряду чётное число членов и имеются два числа, расположенные в середине ряда: 78 и 82. Найдём среднее арифметическое этих чисел:
Говорят, что медианой рассматриваемого упорядоченного ряда, а также исходного ряда данных, записанного в таблице, является число 80.
Если в упорядоченном числовом ряду содержится 2n - 1 членов, то медианой ряда является n-й член, так как n - 1 членов стоит до n-го члена и n - 1 членов — после n-го члена. Если в упорядоченном числовом ряду содержится 2n членов, то медианой является среднее арифметическое членов, стоящих на n-м и n + 1-м местах.
|
|
|




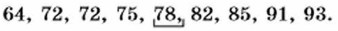

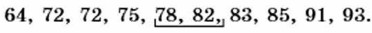
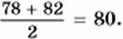 Число 80, но являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы — слева от него находятся пять членов ряда и справа тоже пять членов ряда:
Число 80, но являясь членом ряда, разбивает этот ряд на две одинаковые по численности группы — слева от него находятся пять членов ряда и справа тоже пять членов ряда: