|
|
|
|
|
§ 4. Статистические характеристики ФормулыВ художественной литературе вам, вероятно, приходилось встречаться с непривычными единицами измерения. Так, например, в книге Жюля Верна «Дети капитана Гранта» читаем: • «Это был ябиру — гигантский журавль английских колоний. Эта птица пяти футов ростом, с чёрным широким клювом конической формы, заостряющимся к концу, в длину он имел восемнадцать дюймов»; • «Во время пробного плавания яхта «Дункан» показала скорость в семнадцать морских миль в час»; • «Роберт узнал, что средняя годовая температура в провинции Виктория достигает +74° по Фаренгейту». Для того чтобы этот текст был понятен, надо знать, как упомянутые здесь единицы измерения, выражающие приближённые значения величин, соотносятся с привычными для вас единицами. Это соотношение выражается следующими формулами: b = 30,48а, где а — длина в футах, b — соответствующая длина в сантиметрах; l = 2,54m, где m — длина в дюймах, l — длина в сантиметрах; р = 1,853m, где m — расстояние в морских милях, р — расстояние в километрах;
Выполнив расчёты, найдём, что в приведённом тексте
Заметим, что при выполнении вычислений удобно пользоваться калькулятором. Значит, в книге Жюля Верна речь идёт о следующих приближённых значениях величин. Высота журавля равна 1,5 м, а длина его клюва — 0,5 м. Яхта «Дункан» шла со скоростью 32 км/ч, а среднегодовая температура в провинции Виктория была равна 23° Цельсия. Приведём пример использования формул в задаче на проценты. Пример 1. Найдём, на сколько процентов увеличится площадь прямоугольника, если его длину и ширину увеличить на 10%.
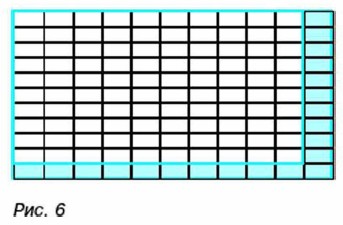
По формуле площади прямоугольника находим, что S = ab. После увеличения длины и ширины прямоугольника на 10% длина будет равна а + 0,1а = 1,1а см, а ширина b + 0.1b = 1,1b см. Тогда площадь будет равна 1,1а • 1,1b = 1,21ab см2, т. е. увеличится на 1,21 ab - ab = 0,21 ab см2. Имеем Этот ответ хорошо поясняет рисунок 6. Из рисунка видно, что к имеющимся 100 малым прямоугольникам, площадь каждого из которых составляет 1% от площади прямоугольника, добавляется ещё 21 малый прямоугольник.
Свойства равенств позволяют из одной формулы, связывающей две или более переменные, получать новые формулы.
|
|
|



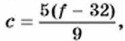 где ƒ — температура в градусах Фаренгейта, с — температура в градусах Цельсия.
где ƒ — температура в градусах Фаренгейта, с — температура в градусах Цельсия.
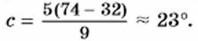
 Пусть длина прямоугольника равна а см, ширина — b см, а площадь — S см2.
Пусть длина прямоугольника равна а см, ширина — b см, а площадь — S см2.
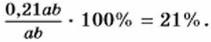 Значит, площадь увеличится на 21%.
Значит, площадь увеличится на 21%.