|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 3233. Корнем уравнения (2х - 3,8) (4,2 + 3х) = 0 являются числа которые обращают в 0 одну из двух скобок. 2х - 3,8 = 0 ⇒ 2х - 3,8 ⇒ х = 1,9. 4,2 + 3х = 0 =+ 3х = -4,2 ⇒ х = -1,4. 1,9 и -1,4 корни уравнения. а) 1,9 является корнем данного уравнения; б) 2 не является корнем данного уравнения; в) -1,4 является корнем данного уравнения; г) -3 не является корнем данного уравнения. 234. а) х2 + 4х + 3 = 0: при х = -4, х2 + 4х + 3 = 16 - 16 + 3 = 3 — не является корнем; при х = -3, х2 + 4x + 3 = 9 - 12 + 3 = 0 — является корнем; при х = -1, х2 + 4х + 3 = 1 - 4 + 3 = 0 — является корнем; при х = 3, х2 + 4х + 3 = 9 + 12 + 3 = 24 — не является корнем; при х = 4, х2 + 4х + 3 = 16 + 16 + 3 = 35 — не является корнем. б) х2 + х - 12 = 0: при х = -4, х2 + х - 12 = 16 - 4 - 12 = 0 — является корнем; при х = -3, х2 + х -12 = = 9 - 3 - 12 = -6 — не является корнем; при х = -1, х2 + х - 12 = 1 - 1 - 12 = -12 — не является корнем; при х = 3, х2 + х - 12 = 9 + 3 - 12 = 0 — является корнем; при х = 4, х2 + х - 12 = 16 + 4 - 12 = 8 — не является корнем. 235. а) 3x + 7 = (9 + х) + 2х ⇒ 3х + 7 = 9 + 3х ⇒ 7 ≠ 9 — уравнение не имеет корней. б) 5x - 1 = 4 • (х + 2) - (9 - х) ≠ 5х - 1 = 4х + 8 - 9 + x ≠ -1 = -1 — корнем уравнения является любое число. в) х2 = х — корни уравнения 0 и 1. г) х + 1 = х - 1 => 1 ≠ -1 — уравнение не имеет корней. 236. а) Потому что модуль любого числа больше либо равен 0; б) |x| + 3 = 0 ⇒ |х| = -3. Потому что модуль любого числа больше либо равен 0. 237. а) |х| = 5 =+ х = ±5. б) |а| -17 = 0 =+ |а| = 17 ⇒ а = ±17. в) 6 - |b| = 0 ⇒ |b| = 6 ⇒ b = ±6. 238. При m ≠ 0 — уравнение имеет единственный корень. При m = 0 — уравнение не имеет решений. Не при каких т уравнение не будет иметь бесконечно много решений.
240. a) 3,8x - (1,6 - 1,2x) = 9,6 + (3,7 - 5x) ⇒ 3,8x -1,6 +1,2x = 9,6 + 3,7 - 5x ⇒ 10x = 14,9 ⇒ х = 1,49; б) (4,5у + 9) - (6,2 - 3,1 у) = 7,2у + 2,8 ⇒ 4,5у + 9 - 6,2 + 3,1у = 7,2у + 2,8 ⇒ 0,4у = 0 ⇒ y = 0; в) 0,6m - 1,4 = (3,5m + 1,7) - (2,7m -3,4) ⇒ 0,6m - 1,4 = 3,5m + 1,7 - 2,7m + 3,4 ⇒ 0,2m = -6,5 ⇒ m = -32,5; г) (5,3а - 0,8) - (1,6 - 4,7а) = 2а - (а - 0,3) ⇒ 5, За - 0,8 - 1,6 + 4,7а = 2а - а + 0,3 ⇒ 9а = 2,7 ⇒ а = 0,3. 241. а) (х - 1) (x - 7) = 0: х - 1 = 0 ⇒ х = 1, х - 7 = 0 ⇒ x = 7 ⇒ x = 1; 7. б) (х + 2) (х - 9) = 0: х + 2 = 0 ⇒ х = -2, х - 9 = 0 = ⇒ x = 9 ⇒ х = -2; 9. в) (х — 11) (х + 6) = 0: х - 11 = 0 ⇒ х = 11, х + 6 = 0 ⇒ х = -6 ⇒ х = -6; 11. г) (х + 1) (х - 1) (х - 5) = 0, х + 1 = 0 ⇒ х = -1, х - 1 = 0 ⇒ х = 1, х - 5 = 0 ⇒ х = 5 ⇒ х = -1; 1; 5. д) х • (х + 3) (х + 3) = 0: х = 0, х + 3 = 0 ⇒ х = -3 ⇒ х = -3; 0. е) (х - 4) (х + 9) (х + 13) = 0: х - 4 = 0 ⇒ х = 4, х + 9 = 0 ⇒ х = -9, х+ 13 = 0 ⇒ х = -13 ⇒ х = -13; -9; 4. 242. а) (х + 5) (х + 6) + 9 = 0 уравнение не может иметь положительный корень, потому что произведение скобок (х + 5) (х + 6) будет положительное число, а оно должно быть равно —9; б) х2 + 3х + 1 = 0 уравнение не может иметь положительный корень, потому что сумма х2 + 3х будет положительное число, а оно должно быть равно -1. 243. а) 0,15 • (х - 4) = 9,9 - 0,3 • (х - 1) ⇒ 0,15х - 0,6 = 9,9 - 0,3х + 0,3 ⇒ 0,45х = 10,8 ⇒ х = 24; б) 1,6 • (а - 4) - 0,6 = 3 • (0,4а - 7) ⇒ 1,6а - 6,4 - 0,6 = 1,2а - 21 ⇒ 0,4а = -14 ⇒ а = -35; в) (0,7х - 2,1) - (0,5 - 2х) = 0,9 • (3х - 1) + 0,1 ⇒ 0,7х - 2,1 - 0,5 + 2х = 2,7х - 0,9 + 0,1 ⇒ 0х = 1,8 — уравнение не имеет решений; г) -3 • (2 - 0,4у) + 5,6 = 0,4 • (3у + 1) ⇒ -6 + 1,2у + 5,6 = 1,2у + 0,4 ⇒ 0у = 0,8 — уравнение не имеет решений. 244. а) 2х + 7 - х + 12 = 14 ⇒ 2х - х = 14 - 12 - х = -5; б) -5у + 1 - (3у + 2) = -9 ⇒ -5у + 1 - 3у - 2 = -9 ⇒ -8у = -9 + 2 - 1 ⇒ -8у = -8 ⇒ у = 1; в) 15х - 1 + 6х - 8 = 15х - 1 - (6х — 8) ⇒ 6х - 8 = -6х + 8 ⇒ 12х = 16 ⇒ х = г) 25р + 1 - (р - 12) - 25р + 1 + р - 12 ⇒ -р + 12 = р - 12 ⇒ 2р = 24 р = 12. 245. 246. 7 • (2х +1) = 13. Так как 13 не делится на 7 без остатка, и скобка 2х +1 при х целом также целое число, корень данного уравнения не является целым. 247. Пусть кроликов х, тогда кур 1000 - х. Так как у кроликов 4 ноги, а у кур 2, значит 4х + 2 • (1000 - х) = 3150 ⇒ 4х + 2000 - 2x = 3150 ⇒ 2х = 1150 ⇒ x = 575 ⇒ 1000 - х = 1000 - 575 = 425. Ответ: 575 кроликов и 425 кур. 248. Пусть на первом участке было посажено х + 9 кустов тогда на втором х. х + 9 + 3 = 1,5 • (х - 3) ⇒ х +12 = 1,5х - 4,5 ⇒ 0,5х = 16,5 ⇒ х = 33 ⇒ х + 9 = 42. Ответ: 42 куста. 249. Пусть у Миши 4х марок, тогда у Андрея х марок. 4x - 8 = 2 • (х + 8) ⇒ 4х - 8 = 2х + 16 ⇒ 2x = 24 ⇒ х = 12 ⇒ 4х = 48. Ответ: у Миши 48 марок, у Андрея 12 марок. 250. Пусть ученик должен был прочитать за t дней книгу, чтобы сдать её в срок. Значит 40?t = (40 - 15) (t + 6) ⇒ 40t = 25 • (t + 6) ⇒ 40t = 25t + 150 ⇒ 15t = 150 ⇒ t = 10. Ответ: за 10 дней. 251. Пусть за t дней артель стеклодувов должна была выполнить заказ. Необходимо было изготавливать в день по 40 деталей, значит всего изготовить надо было 40? деталей. Но так как они изготавливали на 20 деталей больше каждый день, они выполнили заказ на 3 дня раньше. Значит (40 + 20) (t - 3) = 401 ⇒ 60t - 180 = 40t ⇒ 20t = 180 ⇒ t = 9. Ответ: за 9 дней. 252. Пусть х — задуманное число. Значит (х + 7) х × 3 - 47 = х ⇒ 3х + 21 - 47 = х ⇒ 2х - 26 ⇒ х = 13. Ответ: 13 задуманное число.
|
|
|



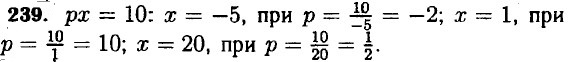
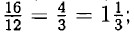
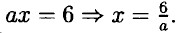 Так как x целое число, значит а ≤ 6 и б должно быть кратным а. Следовательно а = ±1; ±2; ±3; ±6.
Так как x целое число, значит а ≤ 6 и б должно быть кратным а. Следовательно а = ±1; ±2; ±3; ±6.