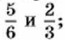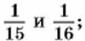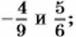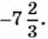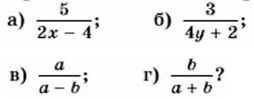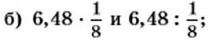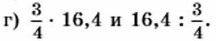Параграф 1

200. Найдите число, обратное:

а) сумме чисел

б) разности чисел 6,2 и 5,8;

в) произведению чисел

г) частному чисел 4,9 и 3,5.

207. Найдите число, противоположное:

а) сумме чисел 2,86 и -4,3;

б) разности чисел

в) произведению чисел -5,75 и 1,6;

г) частному чисел 46 и

208. Найдите сумму всех целых чисел от 102 до 104.

209. Найдите произведение всех целых чисел от -11 до 13.

210. Найдите значение выражения:

211. Известно, что при некоторых значениях а и Ь значение выражения 2(а + Ь) равно -8,1. Найдите при тех же значениях а и Ь значение выражения:

а) 3(а + b);
б) -0,5(а + b);

в) 4а + 4b;
г) -5а - 5b.

212. При каких значениях переменных не имеет смысла выражение:

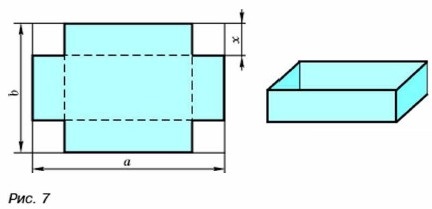
213. Составьте выражение для решения задачи:

а) Периметр прямоугольника 16 см, одна из его сторон т см. Какова площадь прямоугольника?

б) Площадь прямоугольника 28 м², а одна из его сторон равна а м. Чему равен периметр прямоугольника?

в) Из двух городов, расстояние между которыми s км, навстречу друг другу одновременно выехали два автомобиля. Скорость одного из них υ₁ км/ч, а скорость другого υ₂ км/ч. Через сколько часов они встретятся?

г) Через какое время мотоциклист догонит велосипедиста, если расстояние между ними s км, скорость велосипедиста υ₁ км/ч, а скорость мотоциклиста υ₂ км/ч?

214. От прямоугольного листа картона со сторонами а см и b см отрезали но углам квадраты со сторонами х см (рис. 7). Из оставшейся части сделали открытую коробку. Заиишите формулу для вычисления объёма V коробки. Вычислите по формуле объём коробки, если a = 35, b = 25, х = 5. Какие значения может принимать переменная х при указанных значениях а и b?

215. Составьте формулу числа: а) кратною 11; б) кратного 21.

216. Чтобы выразить в километрах расстояние, измеренное в морских милях, пользуются формулой у = 1,853x, где х — расстояние в милях, а у — то же расстояние в километрах. Выразите в километрах следующие расстояния: 10 миль, 50 миль, 250 миль.

217. Сравните:

а) 3,48 - 4,52 и -8,93 + 0,16;

в) 4,7 - 9,65 и 4,7 - 9,9;

218. Верно ли, что:

а) если а > 0 и b > 0, то ab > 0;

б) если ab > 0, то а > 0 и b > 0?

219. Верно ли, что для любых чисел а и b:

а) |а + b| = |а| + |b|; б) |аb| = |а| • |b|?

220. Известно, что |х| = |у|. Верно ли, что х = у?

221. Известно, что |а| < |b|. Верно ли, что а < b?

222. Известно, что |а| > |b|. Возможно ли, чтобы было а < b?

Решенния >>>