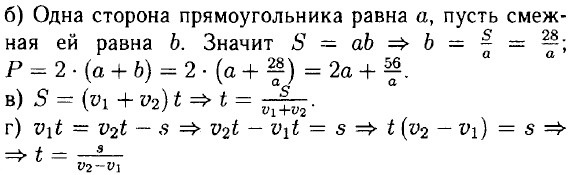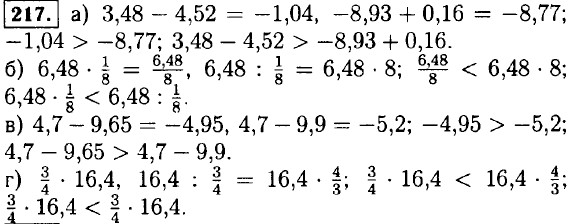|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Дополнительные упражнения к параграфу 1
208. Сумма числа и противоположного ему равна 0. Рассмотрим все отрицательные целые числа от -1 до -102 и противоположные им целые числа от 1 до 102 соответственно, их сумма равно 0. Значит сумма целых чисел от -102 до 104 равна 103 + 104 = 207. 209. Рассмотрим все целые числа от -11 до 13. Одно из этих чисел равно 0, а так как любое число, умноженное на 0 равно 0. Значит и произведение всех целых чисел от -11 до 13 равно 0.
211. 2 • (а + b) = -8,1 ⇒ а + b = -4,05: а) 3 • (а + b) = 3 • (-4,05) = -12,15; б) -0,5 • (а + b) = -0,5 • (-4,05) = 2,025; в) 4а + 4b = 4 • (а + b) = 4 х (-4,05) = -16,2; г) -5а - 5b = -5 • (а + b) = -5 х (-4,05) = 20,25. 212. Выражение не имеет смысла, когда знаменатель равняется нулю,
213. а) Периметр прямоугольника Р есть удвоенная сумма его смежных сторон. Если одна сторона равна m, то другая отличная от неё равна:
214. Длинна коробки: a - 2x = 35 - 10 = 25. Ширина коробки: b - 2x = 25 - 10 = 15. Высота коробки: х = 5. Объём коробки: V = а • b • х = 25 • 15 • 5 = 1875. 2х должно быть меньше b, чтобы получилось сделать коробку. Значит: b > 2х, 12,5 > х > 0. 215. а) х = 11п, где n — любое целое число; б) х = 21n, где n — любое целое число. 216. у = 1,853x. х = 10 миль, у = 1,853х = 1,853 • 10 = 18,53 км. х = 50 миль, у = 1,853x = 1,853 • 50 = 92,65 км. х = 250 миль, у = 1,853x = 1,853 • 250 = 463,25 км.
218. а) верно; б) не верно. Пример: а = -1b = -10 и ab = 10 > 0. 219. а) не верно. Пример: а = 10, b = -1; |а + b| = 9 ⇒ |а| + |b| = 11. б) верно. 220. He верно. Пример: x = 10, у = -10. |x| - |у| = = 10. Но х ≠ у. 221. Не верно. Пример: а = -1, b = -10. |а| < |b|. Но а > b. 222. Возможно. Пример: а = -10, b = -1, b > а и |а| >|b|.
|
|
|



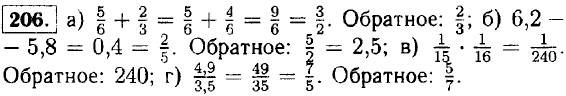
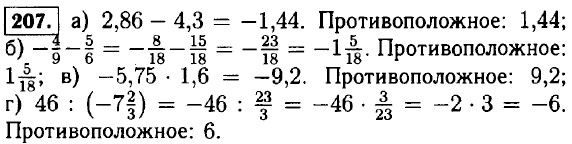
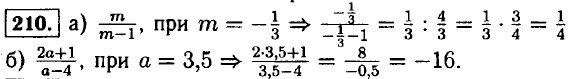
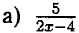 ⇒ 2х - 4 = 0 ⇒ 2x = 4 ⇒ х = 2 — при х = 2 выражение не имеет смысла
⇒ 2х - 4 = 0 ⇒ 2x = 4 ⇒ х = 2 — при х = 2 выражение не имеет смысла
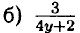 ⇒ 4y + 2 = 0 ⇒ 4y = -2 ⇒ у = -0,5 — при у = -0,5 выражение не имеет смысла.
⇒ 4y + 2 = 0 ⇒ 4y = -2 ⇒ у = -0,5 — при у = -0,5 выражение не имеет смысла.
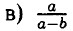 ⇒ а - b = 0 ⇒ a - b — при а = b выражение не имеет смысла.
⇒ а - b = 0 ⇒ a - b — при а = b выражение не имеет смысла.
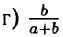 ⇒ а + b = 0 ⇒ а = -b — при а = -b выражение не имеет смысла.
⇒ а + b = 0 ⇒ а = -b — при а = -b выражение не имеет смысла.
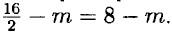 Площадь прямоугольника S равна произведению его смежных сторон. Значит S = (8 - m) • m = 8m - m2.
Площадь прямоугольника S равна произведению его смежных сторон. Значит S = (8 - m) • m = 8m - m2.