График функции (продолжение)

График даёт наглядное представление о зависимости между величинами. Так, по графику температуры воздуха можно узнать, когда температура равнялась нулю, была выше нуля, ниже нуля, возрастала, убывала и т. д. Например, с помощью графика, изображённого на рисунке 8, можно определить, что температура была равна 0 °С в 9 ч и в 22 ч; была положительной с 9 до 22 ч; возрастала с 3 до 15 ч.

На практике часто используются приборы для автоматической регистрации хода того или иного процесса (изменения в течение суток атмосферного давления, изменения в течение суток уровня моря, изменения давления пара в цилиндре двигателя в зависимости от положения поршня). Эти приборы вычерчивают графики соответствующих функциональных зависимостей. Так, с помощью кардиографа получают графическое описание работы сердца, сейсмограф позволяет получить графическое описание колебаний земной поверхности.

Упражнения

283. Функция задана формулой у = х(х - 3), где -2 ≤ х ≤ 2. Заполните таблицу и постройте график этой функции.

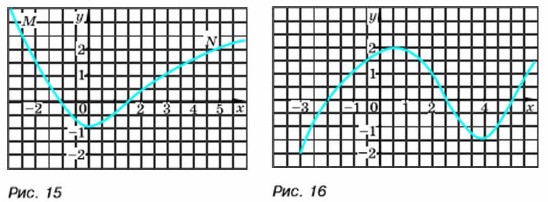
284. Принадлежат ли точки A(4; 2), В(1; -4) и C(1; 4) графику функции, заданной формулой у = 2х - 6? Укажите две точки, одна из которых принадлежит этому графику, а другая нет.

285. Кривая MN — график некоторой функции (рис. 15). Найдите по графику значение функции, соответствующее значению аргумента -2; -1; 0; 1; 5.

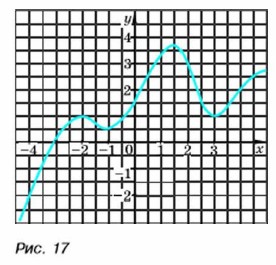
286. Используя график функции (рис. 16), заполните таблицу:

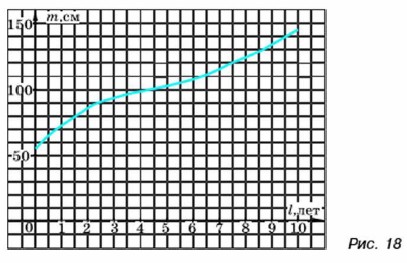
Укажите пять значений аргумента, которым соответствуют положительные значения функции, и пять значений аргумента, которым соответствуют отрицательные значения функции.

287. (Для работы в парах.) Кривая, изобиженная на рисунке 17, — график некоторой функции.

Используя график, найдите:

а) значения у при х = -3; -2; 0; 2; 4;

б) значения х, которым соответствуют у = -2; 0; 2; 3.

1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их.

2) Проверьте друг у друга правильность выполнения задания.

3) Исправьте ошибки, если они допущены.

4) Обсудите возможность существования двух искомых значений в случае а) и в случае б).

288. Пользуясь графиком функции, изображённым на рисунке 17, укажите два каких-либо значения аргумента, при которых функция принимает:

а) положительные значения;

б) отрицательные значения.

289. Измеряя в течение десяти лет каждый год в день рождения рост ребенка, построили график зависимости роста от возраста ребёнка (рис. 18). Пользуясь графиком, найдите:

а) каков был рост ребёнка в 3 года; в 6 лет; в 9 лет;

б) на сколько сантиметров вырос ребёнок за первые пять лет жизни; за последующие пять лет жизни.

<<< К началу Окончание >>>