|
|
|
|
|
Глава 2. Функции График функцииРассмотрим функцию, заданную формулой
где -2 ≤ х ≤ 3. По этой формуле для любого значения аргумента можно найти соответствующее значение функции. В таблице указаны некоторые значения аргумента и соответствующие им значения функции:
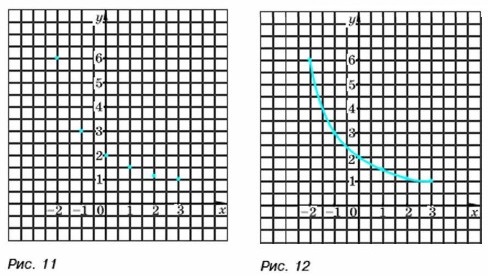
Каждую из найденных нар значений х и у изобразим точкой в координатной плоскости, считая значение д: абсциссой, а соответствующее значение у ординатой (рис. 11). Выбирая другие значения х из промежутка от -2 до 3 и вычисляя соответствующие им значения у по формуле
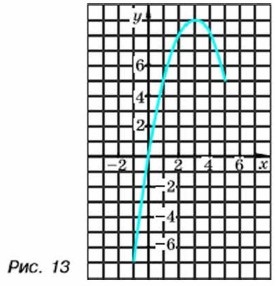
Пример 1. Построим график функции, заданной формулой У = x(6 - х), где -1 ≤ х ≤ 5.
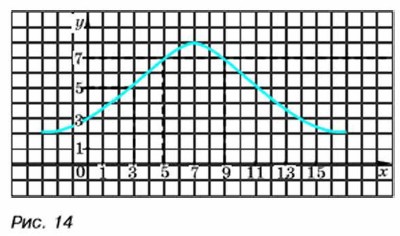
Отметим в координатной плоскости точки, координаты которых указаны в таблице. Соединим их плавной линией (рис. 13). Получим график функции, заданной формулой у = х(6 - х), где -1 ≤ х ≤5. Чем больше отметим точек, принадлежащих графику, и чем плотнее они будут расположены, тем точнее будет построен график функции. С помощью графика функции по значению аргумента можно найти соответствующее значение функции. Можно также решить обратную задачу: но значению функции найти те значения аргумента, которым оно соответствует. Пример 2. По графику функции, изображённому на рисунке 14, найдём: а) значение функции при х = 3; б) значения х, при которых значение функции равно 7.
б) Проведём через точку оси у с ординатой 7 прямую, параллельную оси х. Эта прямая пересекает график в двух точках: с координатами (5; 7) и (9; 7). Значит, функция принимает значение, равное 7, при х = 5 и при х = 9.
|
|
|



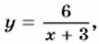

 Составим таблицу соответственных значений аргумента и функции:
Составим таблицу соответственных значений аргумента и функции: