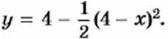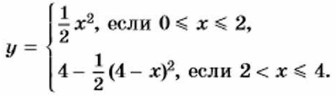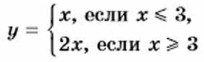|
|
|
|
|
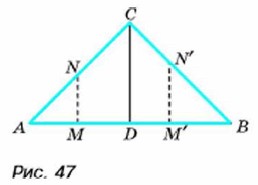
§ 6. Линейная функция Задание функции несколькими формулами (продолжение)Пример 3. На рисунке 47 изображён равнобедренный треугольник AВС, в котором ∠C = 90°, гипотенуза АВ = 4 см. Отрезок MN, перпендикулярный AВ, движется так, что точка М перемещается от точки А до точки В. При этом длина отрезка AM, равная х см, изменяется от 0 до 4 см.
Покажем, что площадь у (в квадратных сантиметрах) отсекаемой отрезком MN фигуры (треугольника AMN или четырёхугольника AM'N'C) является функцией длины отрезка, зададим эту функцию формулами и построим её график. При этом воспользуемся формулой площади треугольника Если переменная х изменяется от 0 до 2 (точка М перемещается от точки А до точки D)y то отсекаемая фигура представляет собой треугольник AMN, площадь которого равна Легко понять, что каждому значению х, где 0 ≤ х ≤ 4, соответствует единственное значение у, т. е. зависимость у от х является функцией. Эту функцию можно задать двумя формулами:
Для построения графика составим таблицу:
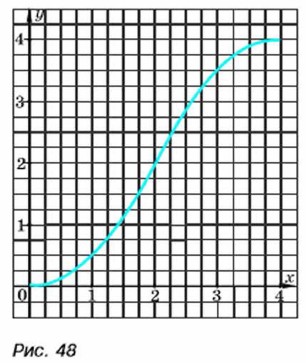
Построив в координатной плоскости точки, координаты которых записаны в таблице, и соединив эти точки плавной линией, получим график рассматриваемой функции (рис. 48).
Замечание. Задавая функцию у = ƒ(x) несколькими формулами, необходимо следить за тем, чтобы каждому значению х соответствовало единственное значение у. В противном случае такая зависимость не будет являться функцией. Например, зависимость
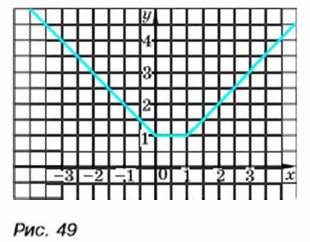
не является функцией, так как в этом случае число 3 — общее значение переменной как для формулы у = х, так и для формулы у = 2х. Поэтому значению х = 3 соответствует не одно, а два значения у : у1 = 3 и у2 = 6. Упражнения 339. Функция задана графиком (рис. 49). Задайте эту функцию аналитически, т. е. одной или несколькими формулами.
|
|
|



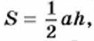 где а — основание треугольника, h — его высота.
где а — основание треугольника, h — его высота.
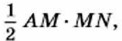 т. е.
т. е. 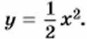 Если же переменная х изменяется от 2 до 4 (точка М' перемещается от точки D до точки В), то отсекаемая фигура представляет собой четырёхугольник AM'N'C, площадь которого равна разности площади треугольника АВС и площади треугольника M'N'B, т. е.
Если же переменная х изменяется от 2 до 4 (точка М' перемещается от точки D до точки В), то отсекаемая фигура представляет собой четырёхугольник AM'N'C, площадь которого равна разности площади треугольника АВС и площади треугольника M'N'B, т. е.