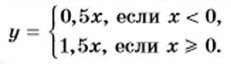|
|
|
|
|
§ 6. Линейная функция
Задание функции несколькими формуламиРанее вы встречались с примерами, когда функция задавалась одной формулой. Однако нередко встречаются ситуации, когда функцию задают несколькими формулами. Приведём примеры. Пример 1. Турист первую часть пути от дома до станции шёл полтора часа со скоростью 6 км/ч. Затем полчаса он отдыхал, а после отдыха оставшуюся часть пути до станции он прошёл за один час со скоростью 5 км/ч. Расстояние s (в километрах) от дома до места нахождения туриста является функцией времени t (в часах). Покажем, что эту функцию можно задать тремя формулами. Когда время t изменяется от 0 до 1,5 ч, расстояние от туриста до дома равно 6/ км, т. е. s = 61, если 0 ≤ t < 1,5. В период от 1,5 до 2 ч расстояние от туриста до дома остаётся неизменным, равным 9 км, т. е. s = 9, если 1,5 ≤ t ≤ 2. Когда время t изменяется от 2 до 3 ч, расстояние от туриста до дома равно 9 + 5(t - 2) км, т. е. s = 5t - 1, если 2 < t ≤ 3. «Это можно записать короче:
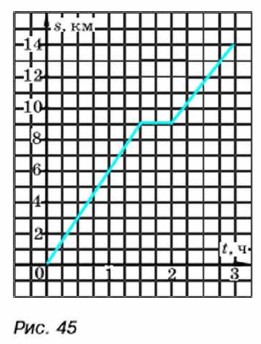
На рисунке 45 изображён график этой функции.
Пример 2. Построим график функции у = х + 0,5 |х|.
у = х - 0,5x = 0,5x при х < 0. Если х ≥ 0, то |х| = х. Значит, у = х + 0,5х = 1,5х при х ≥ 0. Итак, данную функцию можно задать двумя формулами:
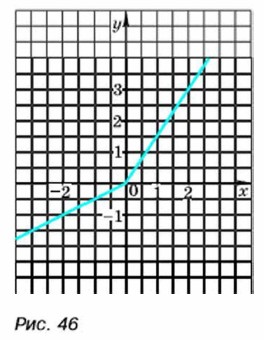
На рисунке 46 изображён график этой функции. Он состоит из двух лучей.
|
Освободимся от знака модуля. Если х < 0, то |x| = -x. Значит,
|
|