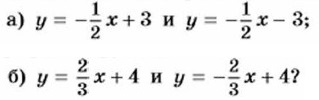|
|
|
|
|
§ 7. Степень и ее свойства Определение степени с натуральным показателем (окончание)389. Окно в старинном особняке имеет форму прямоугольника, завершающегося полукругом (рис. 57). Составьте формулу для вычисления его площади S (в квадратных сантиметрах), если известно, что основание прямоугольника равно а см, высота прямоугольника в полтора раза больше основания. Найдите площадь окна, если а = 80. (Указание. Площадь круга равна πr2, где r — радиус круга, π ≈ 3,14.)
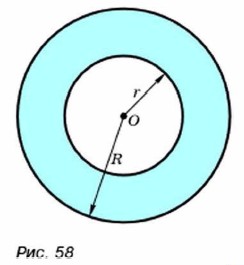
390. Составьте формулу для вычисления площади кольца, изображённого на рисунке 58. Найдите площадь кольца, если R = 6,4 см, r = 3,6 см.
391. Найдите значение выражения: а) 0,01y4 при у=-2; 2; -3; 3; -10; 10; б) 2с2 + 3 при с = -11; 11; 0; -15; 15. 392. Чему равны значения выражений: а) x2; -x2; (-х)2 при x = -9; 9; -6; 6; -2; 2; б) х3; -х3; (-х)3 при х = -4; 4; -3; 3; -1; 1? 393. Вычислите значение выражения х5 + х4 + х3 + х2 + х при x = -1; 0; 10. 394. (Задача исследование.) Найдите всевозможные значения а, где а — натуральное число, при которых число 90 является наименьшим общим кратным чисел 15 и а. 1) Разложите на простые множители каждое из чисел 90 и 15. 2) Обсудите, какие множители должны входить в разложение числа а. 3) Сделайте вывод о значениях числа а. 395. Представьте произведение в виде степени с основанием а: а) а3а; б) а4а2; в) а3а6; г) а20а12. 396. Объясните, почему при любых значениях переменной х значения выражений 4х2 и (х - 8)2 являются неотрицательными числами. 397. (Для работы в парах.) Даны выражения: а2 + 1, -а4, 3 + (5 - а)2, -а - а3, -а2 + 8, 3а + 4, а4 + а2 + 8, -а6 - 4а8 - 1, -7а - 4, -а8 - 9. Какие из этих выражений принимают: а) только положительные значения; б) только отрицательные значения? 1) Распределите, кто выполняет задание а), а кто — задание б), и выполните их. 2) Проверьте друг у друга, верно ли выполнено задание. 3) Исправьте ошибки, если они допущены. 398. Запишите в виде выражения: а) квадрат суммы чисел х и 1; б) сумму квадратов чисел а и b; в) разность квадратов чисел m и n; г) квадрат разности чисел m и n; д) удвоенное произведение квадратов чисел х и у; е) удвоенное произведение куба а и квадрата b. 399. Прочитайте выражение:
Упражнения для повторения 400. Не выполняя построения, найдите координаты точек пересечения графика функции у = 1,2х - 30 с осью х и осью у. 401. Найдите координаты точки пересечения графиков функций: а) у = -4х + 1,3 и у = х - 2,7; б) у = -х + 8,1 и у = -3х + 7,9. 402. Каково взаимное расположение графиков функций:
|
|
|