|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Домашние работы Выражения с переменными32. Объём куба изначально равен был а3. После отрезания прямоугольного параллелепипеда высота уменьшилась на h. Объём искомой фигуры равен (а - К) • а2. 33. В 250 г водного раствора содержалось х г соли, после добавления в него 5 г соли вес всего водного раствора стал равен 250 + 5 = 255 г, а содержание соли в нем стало 5 + х г. Значит концентрация раствора стала 34. В сплаве олова и свинца массой 20 кг содержалось х кг олова, после добавления туда 2 кг олова масса сплава стала 20 + 2 = 22 кг а содержание олова стало х + 2. Процентное содержание олова в сплаве равно 35. а) площадь прямоугольника; б) периметр этого прямоугольника; в) полупериметр; г) удвоенная длинна. 36. а) стоимость одного карандаша и одной тетради; б) стоимость трёх тетрадей и одного карандаша; в) стоимость двух тетрадей и трёх карандашей; г) во сколько раз стоимость тетради больше стоимости карандаша. 37. 1 а) произведение m и x; б) сумма 10 и произведения а и b; в) произведение суммы а и 5 и х; г) разность m и произведения 8 и а; д) сумма произведения 2 и х и 1; е) сумма частного а и b и числа с; ж) сумма произведения а и b и произведения b и с; з) произведение разности а и b и суммы а и b. 38. а) b + с; б) а - m; в) х2, г) у3, д) х + a • b; 39. а) имеет смысл, для любого у; б) имеет смысл, при х ≠ 0, так как при х — 0 знаменатель равняется нулю; в) имеет смысл, при х ≠ 7, так как при х = 7 знаменатель равняется нулю; г) имеет смысл, для любого m; д) имеет смысл, при х ≠ —3, так как при х = — 3 знаменатель равняется нулю; е) имеет смысл, при х ≠ 10, так как при х = 10 знаменатель равняется нулю. 40. 1. Не имеет смысла при а — 9. Так как при а = 9 знаменатель равняется нулю. 2. Не имеет смысла при а = —4. Так как при а = —4 знаменатель равняется нулю. 3. Не имеет смысла при а = 0. Так как при а — 0 знаменатель равняется нулю. 4. Имеет смысл при любых значениях а. Так как знаменатель никогда не равен нулю. 41. а) 5 • n, где n ∈ Z; б) 10 • n, где n ∈ Z; в) 101 • n, где n ∈ Z. 42. 7 • n, где п ∈ Z; n = 100, 7 • 100 = 700 — трёхзначное число кратное 7; n = 101, 7 • 101 = 707 — трёхзначное число кратное 7. 43. 6 = 3 • 2 — для того чтобы число делилось на 6 необходимо и достаточно чтобы число делилось на 2 и на 3. 2 — единственное простое чётное число, а так как мы рассматриваем простые числа, начиная с 5, то все рассматриваемые простые числа являются нечётными. Прибавление или вычитание единицы изменяет чётность. Поэтому всякое простое число, начиная с 5, увеличенное или уменьшенное на 1, делиться на 2. Так как исходное число простое, начиная с 5, значит оно не делиться на 3, обозначим его переменной х. Очевидно, что х — 1 либо х + 1 делиться на 3, так как точно одно из 3 последовательный чисел делиться на 3.
45. х — литров молока было в бидоне первоначально. После того как из бидона отлили 30% молока в нём осталось 70% от первоначального количества, что составило 14 л. 46. х — количество станков, которое должен был выпустить завод по плану.
|
|
|



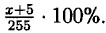 Ответ: 4%.
Ответ: 4%.
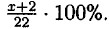 Ответ:
Ответ: 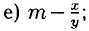 ж) (а + b) • с; з) а • (х + у).
ж) (а + b) • с; з) а • (х + у).
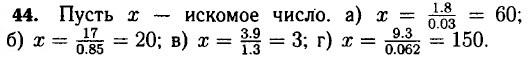
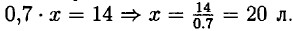 Ответ: 20 литров.
Ответ: 20 литров.
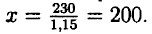 Ответ: 200 станков.
Ответ: 200 станков.