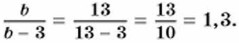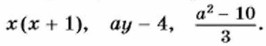|
|
|
|
|
§ 1. Выражения Выражения с переменнымиДвигаясь со скоростью 60 км/ч, автомобиль за 2 ч пройдёт 60 • 2 км, за 3 ч — 60-3 км, за 5 ч — 60 • 5 км, за 5,5 ч — 60 • 5,5 км. Вообще за t ч он пройдёт 60 • км. Изменяя значение t, мы можем с помощью выражения 60/ находить путь, пройденный автомобилем за разные промежутки времени. Для этого достаточно вместо буквы t подставить её значение и выполнить умножение. Букву t в выражении 60t называют переменной, а само выражение 60t — выражением с переменной. Приведём ещё пример. Пусть длины сторон прямоугольника равны а см и b см. Тогда его площадь равна ab см2. Выражение ab содержит две переменные а и b. Оно показывает, как находить площадь прямоугольника при различных значениях а и b. Например: если а = 8 и b =11,то аb = 8 • 11 = 88; если а = 25 и b = 4, то ab = 25 • 4 = 100.
Так, число 88 есть значение выражения ab при a = 8 и b = 11, число 100 есть значение этого выражения при а = 25 и b = 4. Рассмотрим выражение При b = 3 значение этого выражения найти нельзя, так как в этом случае делитель b - 3 равен нулю. Говорят, что при b ≠ 3 выражение Некоторые выражения имеют смысл при всех значениях переменных. Примерами могут служить выражения
Выражения с переменными используются для записи формул. Рассмотрим примеры. Любое чётное число m можно представить в виде произведения числа 2 и целого числа n, т. е. m = 2n. Если в эту формулу вместо n подставлять целые числа, то значениями переменной m будут чётные числа. Формулу m = 2n называют формулой чётного числа. Формулу m = 2n + 1, где n — целое число, называют формулой нечётного числа. Аналогично формуле чётного числа можно записать формулу числа, кратного любому другому натуральному числу. Например, формулу числа, кратного 3, можно записать так: m = 3n, где n — целое число. Упражнения 19. Найдите значения выражения: а) 4х - 12 при х = 7; 0; -5; б) 2,8 - 0,5у при у = 3; 0; -6. 20. Заполните таблицу, вычислив значения выражений 3x - 1 и -3x + 1 для указанных значений х:
Какими числами являются соответственные значения выражений 3x - 1 и -3x + 1? 21. Найдите значения выражений 10 - 2y и 10 + 2у и запишите их в соответствующие клетки таблицы:
|
|
|



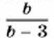 . При любом b ≠ 3 можно найти его значение. Например, если b = 13, то
. При любом b ≠ 3 можно найти его значение. Например, если b = 13, то