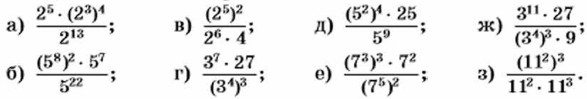Главная >> Алгебра 7 класс. Макарычев. ГДЗ

§ 7. Степень и ее свойства

Возведение в степень произведения и степени (окончание)

441. Представьте в виде степени с основанием а:

а) аⁿа³; б) аа^m; в) а²а^m;

г) (a²)^m; д) (an)³; е) (а³)ⁿ.

442. Представьте в виде степени с основанием 5 число:

а) 25⁴; б) 125³; в) 625².

443. Представьте число 2²⁰ в виде степени с основанием:

а) 2²; б) 2⁴; в) 2⁵; г) 2¹⁰.

444. Запишите число 2⁶⁰ в виде степени с основанием:

а) 4; б) 8; в) 16; г) 32.

445. Выражение а¹² представьте в виде степени несколькими способами.

446. Известно, что а² = m. Найдите а⁶.

447. Упростите выражение:

а) х3 • (х2)5; б) (а3)2 • а5;

в) (а2)3 • (а4)2; г) (х2)5 • (x5)2;

д) (m2m3)4; е) (х4x)2.

448. Запишите в виде степени с основанием а выражение:

а) (a2)4; б) а3 • (а3)2;

в) (а5)2 • (а2)2; г) (а3)3 •(а3)3;

д) (а3а3)2; е) (аа6)3,

449. Упростите выражение:

а) x5 • (х2)3; б) (х3)4 • x8;

в) (х4)2 • (х5)3; г) (х2)3 • (x3)5;

д) (X3)2 • (x4)5; е) (х7)3 • (X3)4.

450. Найдите значение выражения:

Упражнения для повторения

451. Известно, что а < 0 и b > 0. Сравните с нулём значение выражения:

а) ab2; б) а3b;

в) а2b; г) ab3;

д) -ab3; е) а2 + b2;

ж) (а + b)2; з) (а - b)2.

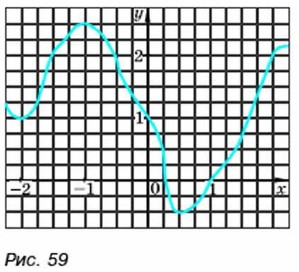
452. Какой цифрой может оканчиваться:

а) квадрат натурального числа;

б) четвёртая степень натурального числа?

453. Известно, что график функции у = kх + 5,4 проходит через точку A(3,7; -2). Найдите значение коэффициента k.

454. На рисунке 59 построен график некоторой функции. Используя график, найдите:

а) значение у при х, равном -2; -1; 2;

б) значения х, при которых у равно -0,5; 2.

Контрольные вопросы и задания

1. Сформулируйте определение степени числа с натуральным показателем. Приведите примеры и назовите в каждом из них основание и показатель степени.

2. Сформулируйте и докажите основное свойство степени.

3. Сформулируйте правило умножения степеней с одинаковыми основаниями. Представьте в виде степени произведение 12 • 12³ • 12⁶.

4. Сформулируйте правило деления степеней с одинаковыми основаниями. Представьте в виде степени частное 5,7⁶: 5,7³.

5. Дайте определение степени числа с нулевым показателем.

6. Сформулируйте правило возведения в степень произведения, правило возведения в степень степени. Представьте в виде степени выражение: (5аb)⁴; (а³)⁶; у⁴ • (y²)⁶.

<<< К началу      Решенния >>>