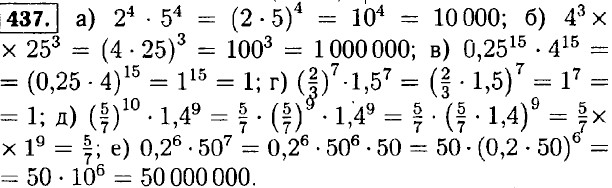|
|
|
|
Главная >> Домашние работы к учебнику Макарычева. Алгебра 7 класс |
|
|
Решенния упражнений Возведение в степень произведения и степени428. а) (ху)4 = х4у4; б) (абс)5 = а5b5с5; в) (2х)3 = 23х3 = 8х3; г) (3а)2 = 32а2 = 9а2; д) (-5х)3 = -53х3 = -125х3; е) (-10аb)2 = -102а2b2 = -100а2b2; ж) (-0,2ху)4 = -0,24х4у4 = -0,0016х4у4; з) (-0,5bd)3 = -0,53b3d3 = -0,125b3d3. 429. a) (mn)5 = m5n5; б) (xyz)2 = x2y2z2; в) (-3у)4 = 34у4 = 81у4; г) (-2аx)3 = -23а3x3 = -8а3х3; д) (10ху)2 = 102х2у2 = 100х2у2; е) (-2аbх)4 = 24а4b4х4 = 16а4b4х4; ж) (-am)3 = -a3m3; з) (-хn)4 = х4n4. 430. а) (2 • 10)3 = 23 • 103 = 8 • 1000 = 8000; б) (2 • 5)4 = 24 • 54 = 16 • 625 = 10000; в) (3 • 100)4 = 34 • 1004 = 81 • 100000000 = 8100000000; г) (5 • 7 • 20)2 = 52 • 72 • 202 = 25 • 49 • 400 = 490000. 431. х противоположное ему число -х. а) (—x)2 = ((-1) • х)2 = (-1)2 • х2 = х2; б) (-x)3 = ((-1)-х)3 = (-1)3 • x3 = -x3. 432. Пусть ребро квадрата а, тогда площадь квадрата равна: S = а2. Если ребро увеличить: в 2 раза, то S = а2 = (2а)2 = 4а2, т. е. площадь увеличится в 4 раза; в 3 раза, то S = а2 = (3а)2 = 9а2, т. е. площадь увеличится в 9 раза; в 10 раза, то S = а2 = (10а)2 = 100а2, т. е. площадь увеличится в 100 раза; в n раза, то S = а2 - (nа)2 = n2а2, т. е. площадь увеличится в n2 раза. 433. Пусть ребро куба а, тогда объём куба равен: V = а3. Если ребро увеличить в 2 раза, то V = (2а)3 = = 8а3, т. е. объём куба увеличится в 8 раз; в 3 раза, то V = (3а)3 = 27а3, т. е. объём куба увеличится в 27 раз; в 10 раза, то V = (10а)3 = 1000а3, т. е. объём куба увеличится в 1000 раз; в n раза, то V = (nа)3 = n3а3, т. е. объём куба увеличится в n3 раз. 434. Пусть ребро куба а, тогда площадь одной грани куба S1 = а2, так как у куба б граней, то площадь всей поверхности S2 = 6а2. Если ребро увеличить в 3 раза, то площадь.всей поверхности станет S = 6(3а)2 = 9S2, что в 9 раз превышает изначальную площадь. Значит и краски должно быть в 9 раз больше, 9 • 40 = 360 г, что меньше 1 кг. Значит 1 кг краски хватит. 435. Пусть ребро куба а, тогда объём куба равен: V = а3. Если ребро увеличить в 2 раза, то объём станет равным V = (2а)3 = 8а3, что в 8 раз превышает первоначальный объём, значит и времени на его заполнение потребуется в 8 раз больше. Так как
436. а) b3x3 = (bx)3; б) а7у7 = (ау)7; в) x2y2z2 = (xyz)2; г) (-а)3b3 = (-аb)3, д) 32а5 = 25а5 = (2а)5; е) 0,027m3 = 0,33m3 = (0,3m)3.
438. а) (x3)2 = х2 • 3 = x6; б) (x2)3 = х2 • 3 = x6; в) (а5)4 = а5 • 4 = а20; г) (а6)3 = а6 • 3 = а18; д) (у2)5 = у2 • 5 = y10, е) (y7)2 = у7 • 2 = у14; ж) (b3)3 = b3 • 3 = b9; з) (b5)2 = b5 • 2 = b10. 439. а) (x6)4 = х6 • 4 = х24; 6) х6х4 = х6 + 4 = х10; в) х2х2 = х2 + 2 = х4; г) (х2)2 = х2 • 2 = х4; д) х2х3х4 = х2 + 3 + 4 = х9; е) ((х2)3)4 = (х2)3 • 4 = (x2)12 = x2 • 12 = х24. <<< К началу Решенния (окончание) >>>
|
|
|



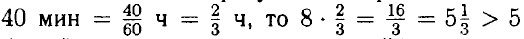 т. е. бассейн на успеет наполнится за 5 часов.
т. е. бассейн на успеет наполнится за 5 часов.