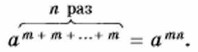|
|
|
|
|
§ 7. Степень и ее свойства Возведение в степень произведения и степениВыражение (ab)4 является степенью произведения множителей а и b. Это выражение можно представить в виде произведения степеней а и b: (ab)4 = ab • аb • аb • ab = (aaaa) • (bbbb) = a4b4. Значит, (ab)4 = a4b4. Аналогичным свойством обладает любая натуральная степень произведения двух множителей.
Сгруппировав отдельно множители а и множители b, получим
Воспользовавшись определением степени, находим
Следовательно, (аb)n = аnbn. 
Доказанное свойство степени произведения распространяется на степень произведения трёх и более множителей. Например: (аbс)n = аnbnсn; (abcd)n = аnbnсndn. Отсюда получается правило:
Пример 1. Возведём произведение 2yz в пятую степень.
Выражение (а5)3 есть степень, основание которой само является степенью. Ото выражение можно представить в виде степени с основанием а: (а5)3 = а5а5а5 = а5 + 5 + 5 = а5 • 3.
Согласно основному свойству степени
Заменим сумму Тогда получим
Следовательно, (аm)n = аmn. Из доказанного свойства степени следует правило:
|
|
|



 По определению степени
По определению степени
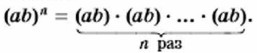
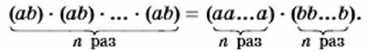
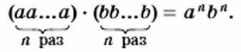
 Имеем (2yz)5 = 25y5z5 = 32y5z5.
Имеем (2yz)5 = 25y5z5 = 32y5z5. 
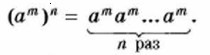
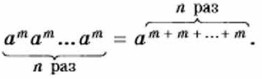
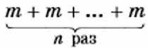 произведением mn.
произведением mn.